William Feller (1906-1970)

Darko Zubrinic, 2006 [in Croatian]

Vilim Feller as a student at the University of Zagreb
with kind permission of prof. Marta Zdenkovic, Zagreb

Abstract. William Feller (Zagreb, 1906 - New York, 1970), outstanding Croatian - American mathematician. At the University of Zagreb completed the first two years of mathematics (i.e. four semesters out of eight, 1923-1925), and then continued his studies in Göttingen where he earned his doctorate (1926). Professor in Kiel, Copenhagen, Stockholm, and Lund. Since 1939 lived in the USA, employed at Universities of Brown, Cornell, and Princeton. One of the founders of Probability Theory as a scientific discipline, best known for his two volume monograph An Introduction to Probability Theory and Its Applications. Many mathematical notions bear his name. Member of several national academies, recipient of the National Medal of Science, USA.

Extended Abstract. William Feller (Zagreb, July 7th, 1906 - New York, January 14th, 1970), outstanding Croatian - American mathematician, born in Croatia as Vilibald Srecko Feller. As a student he simplified the name to Vilim. At the University of Zagreb studied mathematics for the first two years (i.e. the first four semesters out of eight, 1923-1925), and then continued his studies in Göttingen where he earned his doctorate in 1926 under Richard Courant. He prepared a part of his thesis already as a student in Zagreb. Professor in Kiel (Germany, 1928-1933), Copenhagen (Denmark, 1933-1934), Stockholm, and Lund (Sweden, 1934-1939). In 1938 he married Clara Nielsen. Since 1939 lived in the USA, employed at Universities of Brown, Cornell, and since 1950 at Princeton University as a Eugen Higgins Professor of mathematics. Feller wrote the review of A.N. Kolmogorov's famous book Grundbegriffe der Wahrscheinlichkeitsrechnung for Zentralblatt für Mathematik in 1934. One of initiators of editing Mathematical Reviews (1939), and one of its first executive directors (1944-1945). One of the founders of Probability Theory as a scientific discipline, best known for his two volume monograph An Introduction to Probability Theory and Its Applications, which is considered as one of the finest mathematical textbooks of the 20th century. It was translated into Russian (with foreword to Volume 1 written by Kolmogorov), Chinese, Spanish, Polish, and Hungarian. About hundred and fifty mathematical notions bear his name: Feller process, Feller transition function, Feller semigroup, Feller's property, Feller Brownian motions, Feller's test for explosions, Lindeberg-Feller condition, Feller operator, Feller potential, Feller measures, indefinite Krein-Feller differential operators, Kolmogorov-Feller equation, etc. At the International Congress of Mathematicians held in 1958 in Edinburgh, Feller delivered a plenary talk "Some new connections between probability and classical analysis." In 1966 he was elected to the international scientific committee which had to choose candidates for the 1966 Fields Medal at the International Congress of Mathematicians in Moscow. Feller had 17 PhD students. Member of several national academies: former Yugoslav (now Croatian) Academy of Sciences and Arts in Zagreb, Royal Danish Academy of Sciences, National Academy of Sciences, USA, American Academy of Arts and Sciences, Boston, and of prestigeous scientific organizations: Royal Statistical Society, London, and The London Mathematical Society (honorary member). Recipient of the 1969 National Medal of Science by the president of the USA (posthumously in 1970). An asteroid was named after him in 1996: 21276 Feller (1996 TF5). On July 17th 1953 William Feller delivered a lecture in Zagreb in Croatian language, under the title "Matematicka teorija difuzije" (Mathematical theory of diffusion). He was in touch with his relatives in Zagreb, as well as with his colleagues at the University of Zagreb. During the post WWII period Feller visited Zagreb on four occasions: in 1953, 1956, 1957 and 1958. According to Vladimir Vranic, professor of mathematics at the University of Zagreb, "not only that Vilim Feller did not hide his Croatian descent, but he was also proud of it."

Ida and Eugen Viktor Feller, parents of William Feller, around 1900
with kind permission of prof. Marta Zdenkovic, Zagreb

Vilim Feller was a son of world's famous pharmacist Eugen Viktor Feller (Lviv, Lamberg 1871 - Zagreb 1936), who built the family house with pharmacy and laboratories (on the photo below) and the farmaceutical factory, both in Donja Stubica near Zagreb in 1901.

The Feller Pharmacy in Donja Stubica ( night photos)

His father initiated the industrial production of Elsa fluid and its variants (soaps, shampoos, shaving creams, balsams, hygienic and cosmetic products, elixirs, etc.), which was a world wide success, sold in the whole of Europe, Asia (Japan and China), Africa (Egypt), and in the USA. See [Fatovic-Ferencic and Ferber-Bogdan] for more information.

Eugen Viktor Feller, Vilim's father, around 1905
with kind permission of prof. Marta Zdenkovic, Zagreb

Eugen Viktor Feller married Ida Oehmichen (1870-1938; Oemichen is her father's second name, and her mother's second name is Pelc or Peltz), of Austrian descent, with whom he had twelve children, among them Vilim Feller. Eugen Viktor's father was David Feller, of Jewish descent, who lived first in Lviv (or Lavov, Lemberg), and then moved to Austria-Hungary, while his mother was Elizabeta (Elsa) Holzer, of Austrian descent. We may note that Viktor Eugen gave the name of Elsa fluid in honour of his beloved mother Elsa.

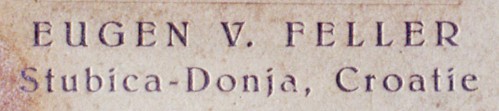
Elsa fluid medicinal soap, Stubica-Donja, Croatie
with kind permission of prof. Marta Zdenkovic, Zagreb

Elsa fluid dom (today Europski dom, Jelacicev trg) in Zagreb (source),
projected by Vjekoslav Basler, built in 1906, with an advertisment of Elsa fluid vial
(photo not later than 1927)

The family of Viktor Eugen Feller contributed to the urban shaping of the city of Zagreb by building three important houses:

• the two storey house at Tomislavov trg 4, built in 1903/1904, projected by Hönigsberg and Deutsch, Imperial and Royal architects (Kaiserlich und Königlich or in short K.u.K.), with a very nice loggia (Venetian Rococo style) along the first and the second floor,
• the four storey Elsa fluid dom built in 1905/1906, at that time the highest building in Zagreb, which is today's European House on the main city square (at the angle of Jelacicev trg and Jurisiceva 1), projected by Vjekoslav Basler (from the Hönigsberg and Deutsch company),
• and the family house built in 1910/1911, a secession styled villa - Feller Haus, in Jurjevska 31a, projected by Mathias Feller, an architect from Munich, Eugen Viktor Feller's halfbrother.

The house of Feller's at Tomislavov trg 4, Zagreb, built in 1904, by H
(photo by D.Z., 2006)

Feller Haus, important secession styled villa in Zagreb, built in 1911,
(photo by D.Z., 2006)

Oval room - Musikzimmer in Feller Haus, Jurjevska 31a, Zagreb

An advertisment for Elsa fluid, published in
Bozicnica, seljacki prosvjetno-politicki sbornik i kalendar za prostu godinu 1927,
ed. by Stjepan Radic, Zagreb 1926, when Willy Feller was at the age of 20.
(Radic's publishing house was in Jurisiceva 1, that is, in the Elsa Fluid dom)

With kind permission of prof. Marta Zdenkovic, Zagreb

Vilim Feller was born on 7 July, 1906 in Zagreb, in time of greatest prosperity of the family. His parents gave him the name of Vilibald Srecko Feller (the Croatian name Srecko is Felix in English). This can be seen in the register of births, Ilica 25, Zagreb (many thanks to prof. Marta Zdenkovic for this information). His address is indicated at Jurisiceva 1, that is, at Elsa fluid dom. The name of Vilibald was given to him according to St Vilibald, ie. St. Willibald, whose feastday is on 7 July. See more information about Sv. Vilibald in Croatian.

The church of St. Marko, Zagreb, where William Feller was baptised;
the roof has been decorated by the Croatian Coat of Arms since 1878 (photo by Hippo);
on the right of the church is the building of the Croatian Parliament (Hrvatski Sabor).

He was baptised on 19th July, 1906 in the church of St. Marko in the Upper Town in Zagreb, by rev. Petar Mrzljak. His godparents were Dr. Miroslav Müller, a physician in the town of Osijek, and his wife Marija. Entering the University of Zagreb in 1923 he simplified his name to Vilim Feller.

Vilibald Srecko Feller in 1907 (?), Zagreb;
with kind permission of prof. Marta Zdenkovic, Zagreb

He was the youngest one of eight brothers, and he also had four sisters (three sisters were born after him):

The huge and hard working family lived happily in Jurjevska 31a, Zagreb, in a beautifully organized house. It was projected by Viktor Eugen's half-brother Mathias Feller, an architect from Munich, Germany. It is interesting that this family building, surrounded with a cultivated park and rare plants, had among others an oval room for music and concerts (Musik-Zimmer). Today the house and the park are in a sad shape, devastated since 1945 during the ex-Yugoslav Communist period.

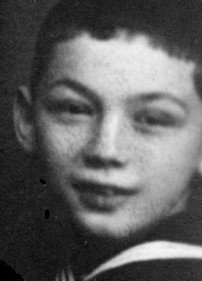Vilibald Srecko Feller (bottom right), the youngest among eight brothers:
Ferdinand, Marko, Vlado, Miroslav, Marian, Kazimir, Dragan, and Vilibald Srecko
(his four sisters were Elsa, Marica, Zora, and Krista)
with kind permission of prof. Marta Zdenkovic, Zagreb

When young Vilibald Srecko Feller was at the age of a secondary school pupil, as a gifted child he had regular private lessons in mathematics from dr. Stanko Vlögel, professor of mathematics and engineering mechanics at the University of Zagreb.

I express my sincere gratitude to dr. Mirna Flögel-Mrsic, professor of biochemistry at the University of Zagreb, for this information (2006). Late professor Stanko Vlögel was her uncle.

The First Gymnasium in Zagreb (now the Mimara Gallery),
where Vilibald Srecko Feller finished his secondary shooling (1922/23);
five of Feller's brothers also finished that school: Ferdinand (1914/15) , Marko (1917/18), Miroslav (1918/19), Marian (1919/20), Vladimir (1919/20).
Photo and data from [Prva Gimnazija u Zagrebu 1854-2004]

Feller finished his secondary schooling in 1923 at the First Gymnasium in Zagreb. He had private lessons, and went to annual exams to that gymansium.

Matriculation form of fourth semester of Vilim Feller's study of mathematics
at the University of Zagreb, 1925,
with kind permission of prof. Marta Zdenkovic, Zagreb

Feller enrolled for the study of mathematics at the University of Zagreb in the academic year 1923/1924. Here is the Matriculation Form issued by the University of Zagreb in 1925, during the second year of his studies of mathematics in Zagreb (during the second semester of the academic year1924/1925), published in [Science in Croatia 2, p. 109]. We underline the fact that the regular study of mathematics lasted for four years. Having completed the first two years of study of mathematics in Zagreb, Feller continued at the University of Göttingen in Germany. According to the obituary published in [The Annals of Math. Statistics], Feller finished his studies at the University of Zagreb with a degree equivalent to today's Master of Science, but this is wrong.

Vilim Feller as a student at the University of Zagreb
with kind permission of prof. Marta Zdenkovic, Zagreb

The content of the 1925 Matriculation Form, filled in by Vilim Feller personally, is as follows:

• which semester enroled: IV
• enrolment date: March 3, 1925
• Faculty: Arts [Mudroslovni, today Filozofski]
• regular student: regular
• the first and second name of student: Vilim Feller
• date of birth: July 7th, 1906
• born in: Zagreb
• domiciled at: Stubica Donja, the Zagreb County
• faith: Roman Catholic
• his mother tongue: Croatian
• his father: Eugen Viktor Feller, pharmacist in Zagreb
• address: Jurjevska 31a
• studied at: Universty of Zagreb
• documents which enable inscription: student's index
• Stipend or support: No

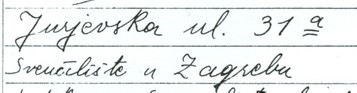
Data filled in in 1925 by Vilim Feller, student of the University of Zagreb

A few names of his professors at the University of Zagreb,
filled in by Vilim Feller in 1925

Now there comes the list of lectures that he attended, with the coresponding names of the lecturers:

• Calculus of Variations, 3 hours (weekly), Dr. Vladimir Varicak
• Mathematical seminar, 3 hours, Dr. Vladimir Varicak
• Number Theory (continued), Dr. Stjepan Bohnicek
• Mathematics IV (+ 2 hours of exercises), Dr. Marije Kiseljak
• Theory of Heat [Nauk o toplini], 3 hours, Dr. Stanko Hondl
• Physical Optics, 1 hour, Dr. Stanko Hondl
• Physical colloquium, 1 hour, Dr. Stanko Hondl
• Exercises in Physics, 2 hours, Dr. Stanko Hondl
• Thermodynamics, 4 hours, Dr. L. Stjepanek
• Mechanics (a continuation), 2 hours, Dr. L. Stjepanek
• Survey of Mathematical Geography, 1 hour, Dr. Milan Senoa
• General didactics, 2 hours, Dr. Stjepan Maticevic
• Signature: Vilim Feller

Personal signature of Vilim Feller in 1925, at the age of 19 
(from a Matriculation form issued by the University of Zagreb)

As we see, young Feller had altogether 29 working hours of lectures weekly (5 days), that is, at the pace of nearly 6 hours each working day.

Vilim Feller in 1925 rowing;
with kind permission of prof. Marta Zdenkovic, Zagreb

A few words about Feller's professors in Zagreb. It is to be noted Dr. Vladimir Varicak at that time was already an established scientist of international reputation, one of the leading European specialists in Einstein's theory of relativity. His very much cited book "Darstellung der Relativitätstheorie im dreidimensionalen Lobatschefskijschen Raume" had been published in Zagreb in 1924 (follow the link for more information), when Feller was on the first year of study of mathematics in Zagreb. Also Stanko Hondl was known as an excellent professor of physics, whose lectures had strong emphasis on concrete experiments.

Stanko Hondl (1873-1971), Feller's professor of physics at the University of Zagreb, was a dean of the Faculty (1919/1920, 1932/1933), rector of the University of Zagreb (1935-1937) , and vicepresident of JAZU (1933-1942, Croatian Academy of Sciences and Arts since 1991); source: Central Physics Library, Zagreb

Dr. Hondl was a successor of professor Vinko Dvorzak, outstanding Czech physicist (and a student of Ernst Mach), who founded the study of physics at the University of Zagreb in 1875. It is very probable that Feller also attanded Hondl's special courses on the theory of relativity and atomic physics, as well as at other professors. Hondl spent an academic year specializing in physics in Göttingen and Berlin (1894-1896), where he also attended lectures delivered by Max Planck. It is very probable that Hondl wrote a recommendation letter for Feller to continue his studies in Göttingen. We mention that also Marije Kiseljak, who lectured Calculus, spent the academic year 1913/14 in Göttingen [Glasnik Mat. Fiz. Astr., 2, 1947, p. 205-209].

University of Zagreb, founded in 1669, where Feller studied from 1923 till 1925
(photos by D.Z., 2007)

Feller's professor Stjepan Bohnicek was a specialist in number theory. He studied mathematics and physics in Vienna, and published among others an extensive paper of almost 60 pages in Mathematische Annalen (Zur Theorie des relativbiquadratischen Zahlkörper, Mathematische Annalen, 63 (1906), 85-144). All this shows that young Feller had good professors, and obtained a solid grounding in mathematics and physics during his studies in Zagreb, which resulted with an equivalent of the title of Master of Science at the very young age of 19.

Here are two more matriculation forms filled in by Vilim Feller (2nd and 3rd semsester, University of Zagreb, 1924 and 1925):

In [Science in Croatia 2, p. 109], in an article by Academician Sibe Mardesic, we can see the names of some other lectures, including mathematical, attended by Feller during the first three semesters (we also exploited the data from the above two matriculation forms; many thanks to Professor Sibe Mardesic):

• Mathematics I, II, III (+ exercises), Dr. Marije Kiseljak
• Infinite series, Dr. Stjepan Bohnicek
• Selected chapters from differential and integral calculus, Dr. V. Varicak
• Number theory, Dr. S. Bohnicek
• Mechanics and acoustics, Dr. Stanko Hondl
• Physics colloquium, Dr. Stanko Hondl
• Exercises in Physics, Dr. Stanko Hondl
• Theory of real functions, V. Vranic
• Theoretical mechanics, Dr. L. Stjepanek
• Psychology, Dr. Albert Bazala
• Anorganic chemistry, V. Pusin
• Organic chemistry, Dr. G. Janecek
• Exercises in organic chemistry, Dr. G. Janecek
• General didactics with introduction to psychology of thinking, Dr. Maticevic
• Psychology of feelings and pedagogical axiology (psihologija cuvstava i pedagogijska aksiologija), Dr. S. Maticevic

A very condensed Repetitorium of Differential and Integral Calculus (in Croatian) by Dr. Marije Kiseljak, 1925, from which the program of Mathematical Analysis for students of mathematics at the University of Zagreb could be seen in time when Feller was a student

David Hilbert (1862-1943), Feller's ideal mathematician;
photo from Hilbert et la conférence de Paris

In 1925, after completing the first two years of study of mathematics in Zagreb, Feller continued at the University of Göttingen, the strongest mathematical center in the world at that time besides Paris. It is natural to assume that this happened under the advice (and recommendation) of his professors in Zagreb. Already the next year, in 1926 (November 3rd), he defended his doctoral thesis Über algebraisch rektifizierbare transzendente Kurven under the name of Willy Feller, at the age of only 20 years, and suma cum laude. His adviser was a famous mathematician Richard Courant, who was a student of David Hilbert. He remained in Göttingen for two years as an assistant of professor Courant. Feller became acquainted with David Hilbert, one of the greatest mathematicians of all times, who was also teaching there. Hilbert was always his ideal mathematician.

Richard Courant (1888-1972), Feller's thesis advisor;
photo from Finite Elements Corner

The archive of the University of Göttingen holds a file about the doctorate of Willy Feller in 1927 (Math.Nat.Prom. 0010, 23). The Faculty of Mathematics and Natural Sciences awarded him a PhD the July 18, 1927 in the disciplines of Mathematics, Analysis and Physics with the above mentioned thesis Über algebraisch rektifizierbare transzendente Kurven (review: Courant). As we have said, in November 3, 1926, the oral exam was held, and members of the committee were R. Courant, G. Herglotz and J. Franck. I express my deep gratitude to Dr. Ulrich Hunger from the Universitätsarchiv Göttingen for this information.

The thesis was published under the same title in Mathematische Zeitschrift in 1928, Vol 27, pp. 481-495.

According to [Vranic, p. 348], Feller already began his scientific work as a student of mathematics in Zagreb, which resulted with the above thesis defended in Göttingen. He reported his original results at the Geometric Seminar led by his professor Marije Kiseljak, Zagreb, who inspired young Feller's interest in this topic.

Ida and Eugen Viktor Feller, Vilim's parents, in 1932 in Bad Gastein spa, Austria;
with kind permission of prof. Marta Zdenkovic, Zagreb

Vilim Feller with his mother Ida, 1932, in Bad Gastein spa, Austria;
with kind permission of prof. Marta Zdenkovic, Zagreb

According to [Reid, Courant in Göttingen, p 111], the assistants of Richard Courant who supervised the mathematical Praktikum in Göttingen discovered at the beginning term in 1925 that there was no longer any need for them to solve problems themselves, since they discovered that the answers of Feller, a new student, were invariably correct.

The assistants promptly alerted Courant to the presence of Willy Feller. After the third calculus lecture, to Feller's amazement, the professor - an unbeleivably august personage to a European student of that day - approached. Questioning the boy about his education in his native land, Courant discovered that Feller was already doing mathematics on his own. He told him to bring his work to the next lecture. Even thus instructed, Feller was too bashful to produce his papers on the appointed day. The next morning he was awakened by commotion on the stairs leading to his attic room. There was a knock on the door. Courant entered and left a few moments later with the desired papers.

After Feller was "discovered" in the Praktikum, he was an accepted member of the new "in group" which gathered around Courant. [Reid, Courant in Göttingen, p 111].

Feller's first scientific work in the domain of Probability Theory was published in 1935 in Mathematische Zeischrift no 40, "Über den Grenzwertsatz der Wahrscheinlichkeitsrechnung, I", at the age of 29.

It seems to be little known that William Feller wrote a review of the famous book by outstanding Russian mathematician A.N. Kolmogorov (1903-1987), Grundbegriffe der Wahrscheinlichkeitsrechnung [English translation of the book], 1933, in which theoretical foundations of Probability Theory have been laid down:

William Feller: Review of Kolmogorov (1933), Zentralblatt für Mathematik und ihre Grenzegebiete, 7:216, 1934.

A.N. Kolmogorov (1903-1988) around 1930,
photo from My Pictures from the History of Mathematics by D.E. Cameron

Here is a part of Feller's review of Kolmogrov's Grundbegriffe for Zentrablatt, taken from [Shaffer and Vovk, p. 56]:

The calculus of probabilities is constructed axiomatically, with no gaps and in the greatest generality, and for the frst time systematically integrated, fully and naturally, with abstract measure theory. The axiom system is certainly the simplest imaginable. . . . The great generality is noteworthy; probabilities in infinite dimensional spaces of arbitrary cardinality are dealt with. . . . The presentation is very precise, but rather terse, directed to the reader who is not unfamiliar with the material. Measure theory is assumed.

It is to be noted that Feller was only 27 years old when this book was published, while Kolmogorov was 30. We need to mention that there exists the Kolmogorov–Feller Equation in Probability Theory. Also, Kolmogorov wrote Foreword to the second Russian edition of Volume I of Feller's famous book An Introduction to Probability Theory and Its Applications.

According to a Swedish mathematician Ulf Grenander (in his interview published in Statistical Science),

The institute [Institute for Insurance Mathematics and Mathematical Statistics in Stockholm, directed by Cramer; D.Z.] had a visitor there from 1936 to 1940, and this was William Feller. Feller came from Germany and Cramer took him under his wings. I think it was Cramer who told him that he should not continue working on differential geometry, which he did before. Cramer advised him to move to probability theory, the field of the future, and then Feller started working on probability theory."

Cramer certainly had impact on Feller, but as we saw, Feller published his first work on probability already in 1935, and Feller was very well acquainted with Kolmogorov's classic monograph, which he reviewd for Zentralblatt. Also, according to Professor Ulrich Krengel, Feller started his work in probability theory already in Kiel, that is, in 1933 at the latest.

Vili Feller with his mother, 1932, in Bad Gastein spa, Austria;
with kind permission of prof. Marta Zdenkovic, Zagreb

Feller defended his habilitation thesis in 1928, and obtained the position of Privat Dozent in Kiel. According to [Croatian Biographical Lexicon] Feller was also a director of the Institute of Applied Mathematics at the University of Kiel. He remained in Kiel until 1933, when he left Germany due to the arrival of Nazism, refusing to sign the Nazi oath. He then continued his carreer in Copenhagen (working at the Mathematical Institute there from 1933 to 1934, where he met also Niels Bohr), and in Stockholm and Lund (from 1934 to 1939; among his colleagues there were Harald Cramér and Marcel Riesz). In 1938 he married Clara Nielsen, who had been his student already in Kiel. In 1939 Feller's emigrated to the USA.

Ida and Eugen Viktor Feller, parents of William Feller,
in Bad Gastein in 1932

Vilim Feller in 1936, when he started to work in Stockholm;
his father Eugen Viktor died the same year in Zagreb, and his mother two years later;
with kind permission of prof. Marta Zdenkovic, Zagreb

In 1937 William Feller participated the celebrated colloquim on probability theory at the University of Geneva, chaired by Maurice Frechét. Feller's paper "Sur les axiomatiques du calcul des probabilités et leurs relations avec les expériences" was published in Wavre (1938–1939), pages 7–21 of the second fascicle, number 735 of Les fondaments du calcul des probabilités. Participants included Cramer, Dœblin, Feller, de Finetti, Heisenberg, Hopf, Levy, Neyman, Polya, Steinhaus, and Wald, and communications were received from Bernstein, Cantelli, Glivenko, Jordan, Kolmogorov, von Mises, and Slutsky. The proceedings were published by Hermann in eight fascicles in their series Actualites Scientifiques et Industrielles. The first seven fascicles appeared in 1938 as numbers 734 through 740. For more information see [Shaffer, Vovk].

According to personal information I obtained from Marta and Nikola Zdenkovic in 2006, Zagreb (their grandfather Ferdinand was William Feller's brother), William Feller was on friendly terms with Albert Einstein (1879-1955), despite a difference of almost 30 years. Since 1950, they were both in Princeton, USA: Einstein at the Institute of Advanced Study and Feller at the Princeton University.

In 1939 Feller became associate professor at Brown University (Providence, Rhode Island), and there he started his work on issuing Mathematical Reviews. In 1944 he became citizen of the USA. In 1945 Feller became a professor at Cornell University, where he worked for five years. In 1950 he obtained the position of Eugene Higgins Professor of Mathematics at Princeton, where he remained until his death in 1970. During the academic years 1965/66 and 1967/68 he lectured as a visiting professor at the Rockfeller University in New York.

Princeton University photos by Mihay

Clara Nielsen, 1937, Feller's student in Kiel (they married in 1938),
with kind permission of prof. Marta Zdenkovic, Zagreb

It is interesting that Feller published two of his scientific works in a Croatian journal, Rad JAZU (JAZU = the then Yugoslav Academy of Sciences and Arts, Zagreb, since 1991 HAZU = Croatian Academy of Sciences and Arts). He wrote both articles in the Croatian language:

• Prilog teoriji mjere u apstraktnim prostorima (Contribution to measure theory in abstract spaces; Bemerkungen zur Masstheorie in abstrakten Räumen), Rad JAZU 249, 1934, 30-45
• O Kolmogoroff - P. Lévyjevu predocivanju beskonacno djeljivih funkcija reparticije (On Kolmogoroff - P. Lévy representation of infinitely divisible distribution functions; Neuer Beweis fur die Kolmogoroff - P. Lévsche Characterisierung der Unbeschränkt teilbaren Verteilungsfunktionen), Rad JAZU, 32, 1939, 1-8.

Under the title of the first article his name is written as follows:

Napisao [written by] Dr. Vilim (W.) Feller

Meanwhile, in 1937 he was elected as corresponding member of JAZU (now Croatian Academy of Sciences and Arts). This is indicated under the title of the second article, where his name is written as

Napisao clan dopisnik [written by corresponding member] Vilim (W) Feller

We provide an excerpt from an article by an American mathematician Michael Golomb, Terror and Exile and a Letter About it (A report from Volume 4, #1, of TopCom), which was a part of a special exhibition organized during the International Congress of Mathematicians in Berlin, 1998:

... The List of Expelled Berlin mathematicians contains 53 names. 21 of them found refuge in US, 7 in GB. Next is the List of Emigrants among all German-Speaking Mathematicians. It contains 130 names. It is a surprise to me, and probably also to many readers, that as many as 75 German mathematicians, many of them world-renowned, emigrated to this country in the thirties. I choose from the list names that are universally recognized: Emil Artin, Reinhold Baer, Gustav Bergman, Felix Bernstein, Lipman Bers, Salomon Bochner, Alfred Brauer, Richard Brauer, Herbert Busemann, Richard Courant, Max Dehn, Willy Feller, Kurt Friedrichs, Kurt Goedel, Hans Hamburger, Ernst Hellinger, Eduard Helly, Fritz John, Theodor Karman, Hans Lewy, Karl Loewner, Kurt Mahler, Karl Menger, Richiird von Mises, Otto Neugebauer, Johann von Neumann, Emmy Noether, Wilhelm Prager, Hans Rademacher, Hans Reichenbach, Arthur Rosenthal, Erich Rothe, Hans Samelson, Otto Schilling, Carl L. Siegel, Otto Szasz, Gabriel Szegö, Olga Taussky, Abraham Wald, Stefan Warschawsky, Wolfgang Wasow, Hermann Weyl, Max Zorn. The great Albert Einstein, himself an emigrant from Berlin, is not included because he is classified as a Physicist, not a mathematician. By their own work and as teachers of a generation of brilliant young American mathematicians these emigrees from Nazi Germany have made the US the great center of mathematics in the world that it is today. ...

Michael Golomb himself left Germany in 1933, went to the Croatian capital Zagreb, and in 1939 arrived to the USA.

William Feller, photo from [Vladimir Vranic]

Professor Ulrich Krengel from the University of Göttingen wrote the following about Feller's participation at International Mathematical Congresses, [History of Probability and Statistics at the International Congresses of Mathematicians, PS]:

... In Oslo (1936 [International Congress of Mathematicians]), Maurice Frechét devoted a portion of his plenary lecture "Mélanges mathématiques" to topics in probability. In addition to his own work, he discussed progress by Hadamard, Hostinsky, Doeblin and Kolmogorov. He also stressed the fact that by now probability was equally exact as other branches of mathematics, and that many mathematical subjects "integral equations, group theory" etc., were used as tools in probability. Another important talk in Oslo was the one given by W. Feller on stochastic processes. He discussed his well known existence and uniqueness theorems for Markov processes with jumps. ...

... In the Conference [International Congress of Mathematicians 1950, Cambridge, Massachussetts] chaired by von Neumann there were three talks related to probability:

• C.E. Shannon: Some topics in information theory
• S.M. Ulam: Random processes and transformations
• W. Feller: Some recent trends in the mathematical theory of diffusion.

Certainly the last of these was a highlight. Feller explained the ties between classical boundary problems for the heat equation and diffusion processes. He also spoke on Ito's theory of stochastic integration. This was possibly the first time that these topics were presented to a broad mathematical public. ...

Vilim Feller (on the right) in Zagreb in 1953, in Jurjevska 31a, where he spent his youth,
with Ivo Zdenkovic, father of Marta and Nikola Zdenkovic
(Ivo's wife Eva is the daughter of Ferdinand, Vilim's brother);
with kind permission of prof. Marta Zdenkovic, Zagreb

At the International Congress of Mathematicians (ICM) held in Edinburgh 1958, William Feller delivered one hour plenary talk "Some new connections between probability and classical analysis", [PDF, 6.8 MB]. For more detailed information see History of Probability and Statistics at the International Congresses of Mathematicians, [PS], by Ulrich Krengel, University of Göttingen, Germany.

Feller was among those who initiated publishing the important Mathematical Reviews journal in 1939, and was one of its first executive editors (1944-1945; the first editors were Otto Neugebauer, 1939-1940, and J.D. Tamarkin, 1940-1944).

Now Mathematical Reviews are published on the web:

According to Ulf Grenander (in his very interesting interview published in Statistical Science), Feller had been the editor of Mathematische Zentralblatt. When he arrived from Stockholm to Brown University (USA) in 1939, he had a complete list of active mathematicians from all over the world with him, and that number at that time was 300! Furthermore,

... Aided by this list, Neugebauer initiated editing the Mathematical Reviews from Brown. Later, Feller took over the editorial responsibilities and continued in that capacity for years until he left Brown and moved to Cornell.

According to the [Annals of Math. Statistics, 1970],

... he [i.e. William Feller] deserves the gratitude of mathematicians for his six years of effort in establishing the new journal [i.e. Math. Reviews], now the leading review of mathematics in the world.

Clara Nielsen Feller, 1957
with kind permission of prof. Marta Zdenkovic, Zagreb

William Feller's monograph An Introduction to Probability Theory and its Applications, Volumes I and II (the first edition appeared in 1950, when Feller was 44), it had subsequent editions, and was translated into several other languages (Russian, Chinese, Polish, Spanish, and Hungarian). It is considered to be one of the best mathematical textbooks written in the 20th century. According to Feller's own words, he worked on Volume I for eight years, since 1941 till 1948.

William Feller: An Introduction to Probability Theory and its Applications, Volume one, John Wiley, New York, 1950

A few quotations from the book:

...Probability is a mathematical discipline whose aims are akin to those, for example, of geometry or analytical mechanics. In each field we must be careful to distinguish three aspects of the theory: (a) the formal logical content, (b) the intuitive background, and (c) applications. The character, and the charm, of the whole structure cannot be appreciated without considering all three aspects in their proper relation. [p. 1]

...Nowadays small boys betting and shooting dice, newspapers report on samples of public opinion, and the magic of statistics embraces all phases of life to the extent that young girls anxiously watch the statistics of their chances to get married. [p. 2]

...The history of probability (and of mathematics in general) shows a stimulating interplay of theory and applications: progress in theory opens new fields of applications, and each new application creates new theoretical problems and influences the direction of research. [p. 3]

William Feller (1906-1970),
photo by Paul Halmos (1916-2006) from his book
I have a photographic memory (Providence, 1987); Halmos provides also the photo of another outstanding Croatian mathematician - Zvonimir Janko

We provide an excerpt from the review of the 1950 first edition of Feller's book (Volume I), written for Mathematical Reviews by R. Fortet:

Afin d'éviter toute notion mathématique élevée (théorie de la mesure, etc.) et pour que l'ouvrage soit utilisable par des étudiants débutants, l'auteur s'est limité aux questions où n'interviennent qu'un nombre dénombrable d'éventualités; mais à propos de ces questions simples il aborde les problèmes les plus avancés de calcul des probabilités, dont beaucoup n'avaient pas encore été exposés dans un livre, de sorte que l'ouvrage est également du plus haut interêt pour les spécialistes. Le texte inclut un très grand nombre d'exemples ou d'exercises proposés, généralement originaux et remarquablement choisis. ...

From the review of the 1957 second edition of Feller's book (Volume I), written by U. Grenander for Mathematical Reviews:

...As in the first edition the exposition is mathematically rigorous and at the same time elegant and lucid. This fascinating book will remain a standard textbook of mathematical probability for many years to come.

From the review of the 1966 first edition of Feller's book (Part II), written by S. Orey for Mathematical Reviews:

This is the sequel to the popular first volume ... but it is designed so that it can be used independently. The reader of this book need not have any prior knowledge of probability beyond a few basic definitions, say as given in the first chapter of the first volume. Indeed it is the author's aim, admirably realized, to be of interest to a diverse audience, ranging from novice to expert. The book has a rich texture, derived from the wealth of problems treated as applications or illustrations of the theory. The striking aspect is the apparent ease and elegance with which these problems are dispatched, frequently making obsolete the original treatment given in the research literature. ...

Photo from The MacTutor History of Mathematics archive, William Feller

As we have said, Feller worked eight years on preparing Volume I of the first edition of his monograph, issued in 1950 (xii+419 pp).

Feller's book: the second edition fourth printing, of the first volume, released in February 1960. Photo from www.biblio.com .

The second volume appeared sixteen years later, in 1966 (xviii+636 pp). Both volumes comprise altogether 1135 pages. Volume I had two more editions, in 1957 (xv+461 pp) and in 1968 (xviii + 509 pp). Both of them were substantially improved with respect to previous editions.

In the Preface to the Volume II of his book, published in 1966, Feller wrote the following:

[speaking about the unexpected success of Volume I] ... The book seems even to acquire new friends. The fact that laymen are not deterred by passages which proved difficult to students of mathematics shows that the level of difficulty cannot be measured objectively; it depends on the type of information one seeks and the details one is prepared to skip. The traveler often has the choice between climbing a peak or using a cable car. ...

Here are the data about the latest editions of both Volumes (from MathSciNet), which comprise altogether 1178 pp:

Feller, William: An Introduction to Probability Theory and Its Applications. Vol. I. Third edition John Wiley & Sons, Inc., New York-London-Sydney 1968 xviii+509 pp.

Feller, William: An Introduction to Probability Theory and Its Applications. Vol. II. Second edition John Wiley & Sons, Inc., New York-London-Sydney 1971 xxiv+669 pp.

The second edition of Volume II was issued in 1971, soon after Feller's death in the Memorial Hospital in New York, January 14, 1970, at the age of 63. His wife Clara wrote on p. xi of the book the following lines:

THE MANUSCRIPT HAD BEEN FINISHED AT THE TIME OF THE AUTHOR'S DEATH, but no proofs had been received. I am grateful to the publisher for providing a proofreader to compare the print against the manuscript and for compiling the index. J. Goldman, A. Grunbaum, H. McKean, L. Pitt, and A. Pittenger divided the book among themselves to check on the mathematics. Every mathematician knows what an incredible amount of work that entails. I express my deep gratitude to these men and extend my heartfelt thanks for their labor of love.

May 1970, Clara N. Feller

See the contents of Volume II of Feller's monograph on Probability Theory.

As we have said, his books have been translated into Russian, Chinese, Polish, Spanish and Hungarian. The first Russian translation of Volume I appeared just a year after the appearance of the book in 1950! And also the first Russian translation of Volume II appeared just a year after the appearance of the book in 1966! Moreover, Feller himself provided corrections of the English 1966 edition for the 1967 Russian edition of Volume II! Here is more detailed information based on Mathematical Reviews:

Russian editions

Feller, V. Vvedenie v teoriyu veroyatnostei i eë prilozeniya. (Diskretnye raspredeleniya.) (Russian) [An introduction to probability theory and its applications. (Discrete distributions.)] Izdat. Inostrannoj Literatury, Moscow, 1951. 427 pp.

Feller, V.: Vvedenie v teoriyu veroyatnostej i ee prilozheniya. Tom 1. (Russian) [An introduction to probability theory and its applications. Vol. 1] Translated from the English by R. L. Dobrusin, A. A. Juskevic and S. A. Molcanov. Edited by E. B. Dynkin, with an introduction by A. N. Kolmogorov. Second edition, reprinted Izdat. ``Mir'', Moscow 1964 and 1967 (reprinted 1964 edition). 498 pp.

Feller, V.: Vvedenie v teoriyu veroyatnostej i ee prilozheniya. Tom 2. (Russian) [An introduction to probability theory and its applications. Vol. 2] Translated from the English by Ju. V. Prohorov Izdat. ``Mir'', Moscow, 1967. 752 pp.

Feller, V.: Vvedenie v teoriyu veroyatnostej i ee prilozheniya. Tom 1. (Russian) [An introduction to probability theory and its applications. Vol. 1] Translated from the third English edition and with a preface by Yu. V. Prokhorov. Second edition. With a preface by A. N. Kolmogorov. ``Mir'', Moscow, 1984. 528 pp.

Feller, V.: Vvedenie v teoriyu veroyatnostej i ee prilozheniya. Tom 2. (Russian) [An introduction to probability theory and its applications. Vol. 2] Translated from the second English edition and with a preface by Yu. V. Prokhorov. Second edition. ``Mir'', Moscow, 1984. 752 pp.

1964 second Russian translation of Feller's Volume 1,
with foreword of A.N. Kolmogorov

From the Foreword to the second Russian edition to Feller's book (Volume I, Moscow 1964), written by A.N. Kolmogorov:

The first edition of Feller's book already obtained a widespread approval in the USSR. Now we bring to the reader's attention the translation of the second English edition, improved and added to by the author in many details. ... It is precisely this choice of material which enables Feller's book to occupy an independent place in the literature on probability theory. ... ... By the choice of problems Feller brings to light their solving by "direct", and specifically probabilistic means. This tendency to see behind analytical transformations their "probabilistic" sense, belongs to the most valuable features of Feller's book. Deserving our attention is also the author's effort in the book in clearly illustrating the character of effects of probabilistic laws on carefully chosen examples . In many cases the author manages to introduce the reader into really interesting questions of comparation between statistical data and probabilistic theory of events. ... (translated from Russian by D.Z.)

Yu. V. Prokhorov in his foreword to the first Russian edition of Volume II wrote the following:

... Professor Feller, having learned about the prepartion of the second volume, kindly sent us a list of many necessary corrections, that were included into the text. I am very grateful to him for his kindness. ... (translated form Russian by D.Z.)

1984 third Russian translation of the third English edition of Volume 1 of Feller's monograph,
also with foreword by A.N. Kolmogorov

It is surprising to read the following sentence of Yu.V. Prokhorov in his foreword to the Russian 1984 translation of the third English edition of Volume 1:

There is no any other book on probability theory comparable to this one - it so successfully comprises mathematical austerity, excellency of proofs, and the quantity of considered applications. Expounding the most complex mathematical questions, the author does not omit from sight the real world phenomena, where a developed theory can be applied. The character of the book is such that it will not age for a very long time. (translated form Russian by D.Z.)

Spanish edition

Spanish translations of both Feller's books have been published in Mexico.

Feller, William: Introducción a la teoría de probabilidades y sus aplicaciones, v. I (504 p.); [version española, Salvador Morales Vaca, Salvador, traductor], México : Limusa-Wiley, 1973

Feller, William: Introducción a la teoría de probabilidades y sus aplicaciones, v. II (738 p.) [version española, Sergio Fernandez Everest], México [etc.] : Limusa, 1985

Many thanks to Dr Radmila Bulajich Manfrino, Mexico, who kindly sent me
scanned pages of the Spanish edition of Feller's books, and to Wasilio Koslow, MSc, Venezuela, for color photos of Feller's books

Polish edition

Feller, William: Wstep do rachunku prawdopodobienstwa. Tom I. (Polish) [Introduction to probability theory. Vol. I] Translated from the second English language edition. Third revised edition (!). Panstwowe Wydawnictwo Naukowe, Warsaw, 1977. 420 pp. First edition in 1966.

Feller, William: Wstep do rachunku prawdopodobienstwa. Tom II. (Polish) [Introduction to probability theory. Vol. II] Translated from the English. Second revised edition (!). Panstwowe Wydawnictwo Naukowe, Warsaw, 1978. 587 pp.

William Feller: Wstep do rachunku prawdopodobienstwa (translated from the Third Edition), Wydawnictwo: PWN, Maj 2007
ISBN: 978-83-01-14684-9
Liczba stron: 456, Tlumaczenie: Robert Bartoszynski

Znakomity podrecznik rachunku prawdopodobienstwa! Wznowienie poszukiwanego od lat klasycznego podrecznika, nalezacego do kanonu literatury dotyczacej ksztalcenia probabilistycznego. Zalety ksiazki to: - prosty i klarowny jezyk, zrozumialy dla absolwentów liceów ogólnoksztalcacych; - liczne zastosowania teorii prawdopodobienstwa w praktyce; - wiele przykladów i zadan; - zadania do samodzielnego rozwiazania z odpowiedziami. Publikacja przeznaczona jest dla studentów nauk scislych, przyrodniczych i ekonomicznych uniwersytetów, uczelni technicznych i akademii pedagogicznych.

In 2006 the first part of Feller's monograph had its 6th Polish edition, so the 2007 edition is already its seventh printing in Poland.

Chinese edition

Feller, William K'ai-lü-lun chi ch'i yin-yung. Ts'e I. (Chinese) [Probability theory and its applications. Vol. I] Translated from the English by Hu Ti-ho and Lin Hsiang-ching Science Press, Peking 1964. xii+253 pp.

William Feller
(in Chinese, from the 1964 Chinese edition of Volume 1)

Many thanks to Professors Sibe and Pavao Mardesic for the above pages of Feller's book in Chinese, 1964, kept in the Library of the School of Mathematical Sciences in Beijing. The 1964 edition has been printed in 9,600 copies, and subsequent Chinese editions seem to exist:

Photo from Book.ChinaUnix.net

The second volume of Feller's monograph has been issued in Chinese in 2007:

William Feller: An Introduction to Probability Theory and Its Applications, Volume 2, Chinese edition, 612 pp, ISBN 978-7-115-16735-4, source www.turingbook.com

Hungarian edition

William Feller: Bevezetés a valószínuségszámításba és alkalmazásaiba, Muszaki Kiadó, Budapest, 1978.

Many thanks to Professor Jozsef Pelikan
from the University of Budapest for his kind help

India

Feller's books have been reedited by Wiley-Eastern, New Delhi, for the needs of mathematicians in India:

• William Feller: An Introduction to Probability Theory and Its Applications . Vol. 1. (Third Edition). Wiley-Eastern, New Delhi. 1993.
• William Feller: An Introduction to Probability Theory and Its Applications , Vol. 2. Wiley-Eastern, New Delhi. 1984.

William Feller with his students; photo by J.R. Goldman, USA.
According to [Halmos, p. 94], Feller "spoke loudly, very fast, with a strong Yugoslav accent [sic! - should be Croatian accent, D.Z.], with wit and charm and understanding."

Feller's scientific interests in mathematics were very broad. He contributed to calculus, geometry, and functional analysis. About half of his papers are in the field of probability theory.

Especially important was his work in the period between 1950 and 1962, when "W. Feller broke new grounds on the theory of diffusion and Kolmogorov was delighted." See [Nitis Mukhopadhyay].

According to Mathematical Reviews, Feller's works are cited 1320 times by 1649 authors. The first part of his book is cited 390 times, and the second part 712 times. It should be noted that Math Reviews is reviewing math articles starting with the year 1939, so that Feller's very productive scientific work before that (that is, between 1926 and 1939) is not evidenced there. His most cited article (37 times) is

Feller, William: The parabolic differential equations and the associated semi-groups of transformations. Ann. of Math. (2) 55, (1952). 468-519. (Reviewer: K. Yosida),

Besides two volumes of his famous book Feller wrote 104 scientific papers, see the complete list in the memorial issue of [Annals of Math. Statistics].

Many mathematical notions bear his name:

The list has been obtained using mathematical references from MathSciNet covering the period between 1970 (since Feller's death) and 2007, citing Feller's name.

Paul C. Kettler, Norway:

...the personal aspects of creative lives are just as important I believe as the professional aspects. At the lowest level, it is personal interaction, after all, which produces great collaborations. Feller and Kolmogorov, across continents and ideologies, is the perfect example.

William Feller has the Erdös number equal to 1 (one): he has a joint paper with Paul Erdös written in 1949 (and with Pollard). Erdös wrote more than 1500 papers, and had 509 coauthors!

Feller-Tornier constant has been defined in Feller's paper written jointly with Erhard Tornier (1994-1982): "Mengentheoretische Untersuchungen von Eigenschaften der Zahlenreihe." Mathematische Annalen, Vol. 107, (1933) 188-232. The constant is defined as the density of natural numbers whose prime factorization contains an even number of distinct primes to powers larger than the first. It is equal to 0.661317... .

Tornier was 12 years older than Feller. In 1932 he became a Nazist, and ousted Feller from the University of Kiel in 1933 when he learned about his Jewish ancestry (for more information see [Thomas Hochkirchen], Abraham A. Fraenkel: Lebenskreise, Deutsche Verlag-Anstalt, Stuttgart, 1967, p. 155, and M. Pinl.: Kollegen in einer dunklen Zeit. III. Jber. Deutsch. Math.-Verein. 73 (1971/72), no. 1, 153-208). Feller had another joint paper with Tornier, published also in Mathematische Annalen, Vol 107, 1933 (Mass und Inhaltstheorie des Bairischen Nullraumes, pp. 165-187), and submitted in 1931.

W. Feller (in white suit) with P. Lévy (sitting) and M. Loeve on his right, and with B. de Finetti on his left, at the 2nd Berkeley Symposium, 1951; photo from Guiseppe Annichini: Bruno de Finetti - a great probabilist and a great man, EMS Newsletter, December 2006

In 1966 Feller had a great honour to become a member of the international scientific committee which had to elect candidates for the 1966 Fields Medal. The committee consisted of Georges de Rham (chair), Harold Davenport, Max Deuring, Willi Feller, Michael Al. Lavrentiev, Jean-Pierre Serre, Donald C. Spencer, and René Thom, see here. Recipients of the Fields Medal at the 1966 International Congress of Mathematicians in Moscow were Michael Francis Atiyah, Alexander Grothendieck, and Stephen Smale.

William Feller with Benjamin Weiss, his PhD student, in 1960s,
from Jay Goldman's Photo Album

Feller is the author or coauthor of two more books:

• Willy Feller: Über die Lösungen der linearen partiellen Differentialgleichungen zweiter Ordnung vom elliptischen Typus, Berlin : Springer, 1929 (when he was teaching in Kiel, Germany)
• Jacob David Tamarkin, Willy Feller (Brown University, Graduate School): Partial differential equations, Providence, R.I., 1941

Feller in 1960s, from Jay Goldman's Photo Album

According to the Mathematical Geneaology Project (with his name indicated as Willi K. Feller), William Feller was thesis advisor to 17 students in the period of 1941 to 1969, and he has as many as 609 descendants. Marta and Nikola Zdenkovic, Zagreb, informed me in 2006 that they do not know the meaning of initial "K." appearing in Feller's name in the Math Geneaology Project, and expressed their doubts about it. However, there exists a paper entitled Feller, W.K., "Statistical aspects of ESP", Journal of Parapsychology, 4 (1940), pp. 271-98. Here are the names of Feller's PhD students:

Feller's unofficial PhD student was Frank Spitzer, see here. His another unofficial PhD student seems to be Joanne Elliott. According to information that I obtained from two independent sources, the family of Feller's adopted Joanne Elliott when she was a grown up girl. She became a professional mathematician, and in one of her papers,

Joanne Elliott: The Boundary Value Problems and Semi-Groups Associated with Certain Integro-Differential Operators, Transactions of the American Mathematical Society, Vol. 76, No. 2 (Mar., 1954), pp. 300-331, doi:10.2307/1990771

she wrote the following: "...This problem, suggested by W. Feller, arises in the theory of stochastic processess. ... The author wishes to thank William Feller for many helpful discussions..." Furthermore, Feller and Elliot published a joint paper:

Joanne Elliott, William Feller: Stochastic Processes Connected With Harmonic Functions, Transactions of the American Mathematical Society, Vol. 82, No. 2 (Jul., 1956), pp. 392-420, doi:10.2307/1993055

Joanne Elliott, photo by Paul Halmos (on the same page Feller's photo appears)
I have a photographic memory (Providence, 1987)

William Feller mentions Joanne Elliott in the Introduction to Volume II of his monograph. In Joanne Elliott math geneaology we can find that the title of her dissertation was On Some Singular Integral Equations of the Cauchy Type, and advisor unknown (Feller?). She earned her PhD at Cornell in 1950, and recall that Feller was professor there in the period of 1945-1950. In Rutgers-New Brunswick Mathematics Graduate Faculty we found that she worked in potential theory, and that in 1974-77 she had a chair at Douglas College (at Rutgers since1964, Professor of Mathematics since 1965), retired since 1991.

William Feller; photo from [Croatian Biographical Lexicon]

Feller became a member of the Croatian Academy of Sciences and Arts in Zagreb (the then JAZU) in 1937, that is, at the age of 31. He was also a member of the Royal Danish Academy of Sciences, and the Royal Statistical Society in London. Shortly before his death he was elected as an honorary memebr of the London Mathematical Society. He was also a governor of the New Jersey section of the Mathematical Association of America (1958-1961, [PDF]), and a president of the Institute of Mathematical Statistics in 1947. According to [Roseblatt, p 12], Feller was a member of the American Philosophical Society.

William Feller was representative of several committees of the American Mathematical Society (AMS), see [PDF]:

• since 1959 till 1961 (two mandates) he was a Representative of the Society (AMS) in the Division of Mathematics of the National Research Council (together with K.O. Friedrichs, P.R. Halmos, Morrey, I. Kaplansky, N.H. Mc Coy, C.B. Morrey, H. Busemann, B.W. Jones)
• a member of Committee to Select One Hour Speakers For Summer and Annual Meetings (with J.W. Green, chairman, and Hans Rademacher)

National Medal of Science, conferred to William Feller in the White House
by president Richard Nixon in 1970 (posthumously)

Feller was a member of the National Academy of Sciences (USA, since 1960) and of the American Academy of Arts and Sciences, Boston, since 1958 (Career description: Mathematician; Educator).

Many outstading mathematicians from Princeton University were elected as members of the National Academy of Sciences: Solomon Lefschetz (1925), James W. Alexander (1930), John von Neumann (1937), Hermann Weyl (1940), Eugene P. Wigner (1945), Salomon Bochner (1950), Howard P. Robertson (1951), Norman E. Steenrod (1956), Emil Artin (1958), William Feller (1960), Donald C. Spencer (1961), John W. Milnor (1963), etc. See the complete list.

Feller was awarded the National Medal of Science of the USA in 1969 (Discipline: Mathematics and Computer Science). The National Medal of Science award was established by the U.S. Congress as a Presidential award. It was conferred in 1970 by president Richard Nixon to Feller's wife Clara during the official ceremony held in the White House, a month after Feller's death at the age of 63. This prestigeous medal has been conferred to him for

• his important contributions to pure and applied mathematics,
• his efforts to make probability theory accessible to broad audience,
• his pioneering work in establishing Mathematical Reviews.

Some mathematicians dedicated their scientific works to the memory of William Feller, for example by his PhD student H.P. McKean:

H.P. McKean. Geometry of differential space: Dedicated to the memory of Will Feller. The Annals of Probability, 1:197-206, 1973.

On July 17th 1953 William Feller delivered a lecture in the building of JAZU, Zagreb, in Croatian language, under the title "Matematicka teorija difuzije" (Mathematical theory of diffusion), see [Mardesic, Some data...].

He was in touch with his relatives in Zagreb, as well as with his colleagues at the University of Zagreb. During the post WWII period Feller visited Zagreb on four occasions: in 1953, 1956, 1957 and 1958 (a letter from 1957, written in Croatian by the mother of Marta and Nikola Zdenkovic, mentions that "uncle Will and Clara" are in Zagreb, and that they have brought toys for Marta and Nikola from the USA).

Department of Mathematics, PMF, University of Zagreb,
Marulicev trg, Zagreb, Croatia, where Feller had a lecture in 1956 (photo by D.Z., 2007)

He helped professor Sibe Mardesic from Zagreb, at that time a young scientist, to spend the academic years 1957/58 and 1958/59 at the Institute for Advanced Study in Princeton, see [here]. S. Mardesic was introduced to Feller in person by Zeljko Markovic in his office, when Feller visited Department of Mathematics and had a lecture there, PMF, Zagreb, in 1956. According to [Vranic, p. 352], "...not only that Vilim Feller did not hide his Croatian descent, but he was also proud of it."

William Feller in 1960s
photo courtesy of professor Mladen Vranic, Toronto

J. Dieudonné, a well known French mathematician, and a member of the Bourbaki group, in his book A panorama of pure mathematics - As seen by N. Bourbaki (Academic Press, New York, London, 1982), indicated that the main ideas of probability theory are related to the names of:

J. Bernoulli (1654-1705), A. de Moivre (1667-1754), P. Laplace (1749-1827), D. Poisson (1781-1840), P. Chebisev (1821-1894), A. Markov (1856-1922), E. Borel (1871-1956), N. Wiener (1894-1959), P. Lévy (1886-1971), A. Kolmogorov (1903-1987), A. Hincin (1894-1959), W. Feller (1906-1970), J. Doob (1910-2004), and G. Hunt (b. 1916).

William Feller in 1964; photo from The MacTutor History of Mathematics archive;
the source is probably [Halmos]

It is amusing that the name of the street in Princeton where William Feller lived since 1950 until his death was

If you go here http://maps.google.com/ and type "Random Road" "Princeton, New Jersey" you will go right to the short road where Prof. Feller and his wife lived. It's just off Nassau St., the main street in Princeton. (Was the name of the street given in honour of Feller? D.Z.)

Many thanks to Mr Paul C. Kettler, Norway, a former student of professor Feller, for this wonderful information (2006). Here is another lovely detail from Feller's lectures, described by Mr Kettler:

Feller's favorite number was "17," employed over and over in his talks whenever a natural number was in order, and the low integers one, two, and three, were not evident choices. This was in expressions such as, "Consider the sum of 17 random variables," etc. This use of "17" was a standing joke, which he loved as much as anybody else.

[This is why some people call number 17 - the Feller number, see Wikipedia; D.Z.] One other anecdote by Mr. Kettler:

Feller and Salomon Bochner each had corner offices on the first floor of the old Fine Hall (now Jones, the Psychology Department.) As there was a central auditorium-style classroom on the floor, offices and smaller classrooms were to the outside of a rectangular hallway around the floor. Bochner's office was in the near right corner as you entered the building, and Feller's was at the next corner continuing. Frequently the two of them, precipitated by a quick phone call from one to the other, would meet in the hall, then march around (always counter-clockwise) several times in very animated discussion. Sometimes they would retire to one or the other's office for more talk, but usually they would not. After three circuits or so they would have exhausted their comments to each other, and would retire back to their offices. It was really a funny, and frequent, sight.

A lovely example of a computation á la Feller is provided by his student Gian Carlo Rota, a well known Italian-American mathematician. One of the first examples of definite integrals computed at the calculus level is integration of the the function sin²x from zero to 2pi. Here is how Feller does it. First integrate the identity sin²x + cos²x = 1 from zero to 2pi, and then note (by a trivial geometric arguement) that both integrals on the left-hand side are equal. Hence, the required integral is equal to pi.

Besides his native Croatian, William Feller spoke also German, English, French, Latin, Hebrew, and very probably Swedish as well (recall that he spent five years in Sweden, from 1934 till 1939). And concerning Feller's fluency in Swedish, here is a testimony of Ulf Grenander, a Swedish mathematician: "... later I had many contacts with him. He used to write to me in Swedish!" According to the information that I obtained from Mr. Nikola Zdenkovic in 2006, his hobby was translating old texts from Sanskrit.

Professor Feller was a member of editorial boards of two prestigeous journals: Transactions of the American Mathematical Society and the Annals of Mathematical Statistics.

William Feller's vivid lecturing, photo by J.R. Goldman, USA
(from the cover of an internal magazine of IBM)

Feller's PhD student Benjamin Weiss has nice memories about his professor:

He was a remarkable mathematician/teacher and person. ... Feller not only taught me probability theory and mathematics, he also introduced me to IBM Research where I worked both during my graduate studies in the summer time and for several years after receiving my degree. Herman Goldstine (a collaborator of J. von Neumann) was the director of Mathematical Sciences at the IBM Research center and he had a number of distinguished mathematicians serve as consultants. These included Courant, Mark Kac, Feller and later on J. Moser. During
my first year of studies when I asked him about math in industry he arranged that I get a summer position at IBM Research which led to my connections with them. ...

Ulf Grenander in his interview for Statistical Science described Feller's character as follows:

He was a very colorful person. I remember that he once explained at a party how World War I really started. His view was quite different from the conventional one. Feller was very entertaining. He was a great storyteller and he told stories about practically anything imaginable.

From an introductory article written by the editorial board of [Annals of Math. Statistics] on the occasion of death of William Feller in 1970, we cite the following:

... His expository lectures and articles have done a great deal to spread the knowledge and recognition of probability throughout the world. His books catch the flavor of his mathematics, though only his presence could convey the full enthusiasm of his lectures. The jacket cover of the third edition of Volume I bears this appreciation from Gian-Carlo Rota of MIT: "... one of the great events in mathematics of this century. Together with Weber's Algebra and Artin's Geometric Algebra this is the finest text book in mathematics in this century. It is a delight to read and it will be immensly useful to scientists in all fields."

In the same issue of the [Annals of Math. Statistics] we can find the following dedication on the separate page:

By action of the Council of the Institute of Mathematical Statistics, the 1970 volume of the Annals of Mathematical Statistics is dedicated to the memory of

WILLIAM FELLER

William Feller, probably in 1940s, when he worked on establishing Math. Reviews;
photo from [Proceedings of the Sixth Berkeley Symposium on Mathematical Statisics and Probability (Univ. California, Berkeley, Calif., 1970/1971), Vol. II: Probability theory]

Mark Kac in his very interesting article [William Feller, In Memoriam], wrote the following lines:

William Feller, one of the most original, accomplished, and colorful mathematicians of our times, died after a long illness on 14 January, 1970. The entire mathematical community mourns his death but at this symposium his loss will be felt more deeply, for all of us here have been influenced both by his work and by his person. ...

Volume I, or to be precise, An Introduction to Probability and its Applications, Volume I, is a book with few peers in scientific literature. It is a treatise and a textbook, a masterpiece of exposition and a credo of methodology of sweeping panorama of a subject and a collection of examplary jewels. No wonder it has appealed to an audience so wide as to border on the incredible, ...

Feller was a man of enormous vitality. Not even in the last stages of his illness was his zest for life visibly lessened. ...

Outside of mathematics and science Feller was especially interested in ancient history - and in this fascinating field his knowledge and competence bordered on the professional. ...

Joseph Doob, a renowned American mathematician, wrote about Feller the following, see his article [William Feller and twentieth century probability]:

... No other book even remotely resembles it in its combination of the purest mathematics together with a dazzling virtuosity of techniques and applications, all written in a style which displays the enthusiasm of the author. This style has made the book unexpectedly popular with nonspecialists, just as its elegance and breadth, not to mention its originality, has made it an inspiration for specialists.

... Those who knew him personally remember Feller best for his gusto, the pleasure with which he met life, and the excitement with which he drew on his endless fund of anecdotes about life and its absurdities, particularly the absurdities involving mathematics and mathematicians. To listen to his lecture was a unique experience, for no one else could lecture with such intense excitement. No one could generate in himself as well as in his auditors so much intense excitement. In losing him, the world of mathematics has lost one of its strongest personalities as well as one of its strongest researchers.

In the same obituary Joseph Doob wrote the following:

Feller (1906-1970) made original and profound contributions to probability theory over a period (from 1935 till his death) over which it was transformed from a poor relation to a central branch of mathematics.

Vilim Feller, photo from [Vranic]
photo by Orren Jack Turner, Princeton University Library

Vilim Feller in 1907 (?), Zagreb;
with kind permission of prof. Marta Zdenkovic, Zagreb

Joe Doob said the following in his conversation with J.L. Snell:

... While writing my book [Stochastic Processes] I had an argument with Feller. He asserted that everyone said "random variable" and I asserted that everyone said "chance variable." We obviously had to use the same name in our books, so we decided the issue by a stochastic procedure. That is, we tossed for it and he won.

... My inclination has always been to look for general theories and to avoid computation. A discussion I once had with Feller in a New York subway illustrates this attitude and its limitations. We were discussing the Markov property and I remarked that the Chapman Kolmogorov equation did not make a process Markovian. This statement satisfied me, but not Feller, who liked computation and examples as well as theory. It was characteristic of our attitudes that at first he did not believe me but then went to the trouble of constructing a simple example to prove my assertion.

Feller was the first mathematical probabilist I had ever met and meeting him at a Dartmouth meeting of the AMS around 1940 I felt like Livingston when Stanley found him in Africa. I envied the Russian probability group but Kolmogorov, who included statisticians among the probabilists, told me around that time how he envied the fact that the US had so many probabilists! ...

Originally I wrote in ink, applying ink eradicator as needed. Feller visited me once and told me he used pencil. We argued the issue, but the next time we met we found that each had convinced the other: he had switched to ink and I to pencil. ...

Richard Feynman, a famous american physicist and Nobel prize winner, wrote in his bestseller "Surely You're Joking Mr. Feynman"!, p. 210, that he liked to talk to Professor Feller at Cornell. Feller worked there from 1945 till 1950, as well as Feynman.

S Ramasubramanian (Bangalore, India, PDF):

William Feller, in the preface to the third edition of his classic, observes that even in the 1940’s few mathematicians recognised probability as a legitimate branch of mathematics and that applications were limited in scope. ...

Let us see a part of autobiographical sketch of a winner of the 1998 Steel Prize awarded by the American Mathematical Society, which only mathematicians can write:

Doron Zeilberger was born on July 2, 1950, in Haifa, Israel, to Ruth (Alexander) and Yehudah Zeilberger. He received his Ph.D. in 1976, from the Weizmann Institute of Science (as a student of Harry Dym (a student of Henry McKean (a student of William Feller (a student of Richard Courant (a student of David Hilbert))))).

See also Zeilberger's article: Fully AUTOMATED Computerized Redux of Feller's (v.1) Ch. III (and Much More!), accompanied by Maple package FELLER.

Professor Donald A. Dawson (Ph.D., MIT, 1963) described his scientific geneaology in a similar way:

...thesis advisor was Henry P. McKean (Ph.D., Princeton, 1955); McKean's thesis advisor was William Feller (Ph.D., Gottingen, 1926); Feller's thesis advisor was Richard Courant (Ph.D., Gottingen, 1910); Courant's thesis advisor was David Hilbert (Ph.D., Konigsberg, 1885).

We learned from Personajes de la Astronomía y la Astronáutica, Venezuela, that there is an asteroid bearing the name of William Feller (1906-1970):

Matemático Croata, nacionalizado estadounidense. Trabajó en matemática probabilística y modificó las relaciones de procesos markovianos y las ecuaciones diferenciales parciales.

Asteroide: (21276) Feller

For a detiled description of the Feller planetoid 21276 Feller (1996 TF5), discovered in 1996, see NASA. There we can see Feller's mini-biography (an anonimous author forgot to mention that Feller taught at Princeton as well):

William Feller (1906-1970) studied at Zagreb and Göttingen and taught at Kiel, Stockholm, Brown University and Cornell University. He was one of the founders of the modern probability theory based on concepts of measure theory.

Here is a list of books on Probability Theory in which Feller's results are mentioned either in chapter or section titles, or in some other way. Many thanks to Professor Sibe Mardesic for this list which he collected (with the help of Dr. Hrvoje Sikic and Dr. Zoran Vondracek, University of Zagreb) for the needs of the exhibition Centuries of Natural Sciences in Croatia, 1996, Zagreb:

Kiyosi Ito and Henry P. McKean, Jr.: Diffusion Processes and Their Sample Paths, Academic Press, Springer Verlag, 1965

... W. Feller has our best thanks, his ideas run through the whole book, and we shall think it a success if it pleases him. (p. XIII)

5.7. Feller's Brownian motions

Kai Lai Chung: Lectures from Markov Processes to Brownian Motion, Springer Verlag, 1982

2.2. Feller Process

Richard Durett: Probability, Theory and Examples, Wadsworth and Brooks, 1991

4 The Lindeberg-Feller Theorem

Daniel Revuz, Marc Yor: Continuous Martingales and Brownian Motion, Springer Verlag, 1991

III. 2. Feller Processes

Paul-André Meyer: Processus de Markov, Springer Verlag, 1967

Chapitre XIII
Semi-groupes de Feller

Jean Dieudonné: A Panorama of Pure Mathematics As Seen by N. Bourbaki,
Academic Press, 1982

7. The Originators
The main ideas in probability theory are due to the following mathematicians: see here, p 227

Stewart N. Ethier and Tomas G. Kurtz: Markov processes, Characterization and Convergence, John Wiley & Sons, 1986

2. Markov Jump Processes and Feller Processes

E.B. Dynkin: Markovskie processy, Gosudarstvennoe izdatel'stvo fiziko-matematicheskoj literatury, Moskva 1963

4. Fellerovskie perehodnye funkcii v kompaktah

L.C.G. Rogers and David Williams: Diffusions, Markov Processes, and Martingales, Volume 1, Cambridge University Press, 1979

Feller-Dynkin (FD) Semigroups, pp. 240-262

The Feller-McKean chain, III-23, III.35

L.C.G. Rogers and David Williams: Diffusions, Markov Processes, and Martingales, Volume 2: Ito Calculus, John Wiley & Sons, 1978

57. Feller Brownian motions

Ioannis Karatzas and Steven E. Shreve: Brownian motion and Stochastic Calculus, Springer Verlag, 1991

5.29 Theorem (Feller's (1952) Test for Explosions)

Aditional refereces:

Kosaku Yosida: Functional Analysis, Grundlehren der mathematischen Wissenschaften 123, Springer-Verlag, 1980 (6th ed.)

XIII. The generalized Laplacian of W. Feller, pp 403-408

The ambitious and voluminous Encyclopedia of Mathematics issued in the former USSR in five books (Matematicheskaya enciklpediya 1-5, Moscow, 1977-1985), has an extensive article entitled Feller process (Fellerovskij process, Volume 5), written by S.N. Smirnov. The author states that Feller processes (introduced in 1952) represent probabilistic generalizations of topological dynamics. The article mentions some other articles and books related to Feller processes, for example, Dynkin and

I.V. Girsanov: Teorija verojatnostej i ee primenenija, 1960, t. 5, No 3, pp. 314-330.

S. H. Lehnigk: The Generalized Feller Equation and Related Topics, Pitman Monographs and Surveys in Pure and Applied Mathematics, Volume 68, Longman, 1993 (304 pp)

Michael Demuth, J.A. Van Casteren: Stochastic Spectral Theory for Selfadjoint Feller Operators: A Functional Integration Approach, Birkhäuser Verlag, 2000

photo from www.allbookstores.com

Radu Zaharopol: Invariant Probabilities of Markov-Feller Operators and Their Support, Birkhäuser Verlag, 2005

photo from www.abeys.com.au

Kai Lai Chung: Chance and Choice: Memorabilia, World Scientific Publishing, 2004, contains Chung's old photo with Feller

Krishna B. Athreya, Soumendra N. Lahiri: Measure Theory and Probability Theory, Springer, 2006

11.1 Lindeberg-Feller theorems

14.2.9.1 Feller continuity

Kiyosi Itô: Essentials of Stochastic Processes, translated from the Japanese 1957 edition by Yuji Ito, published by American Mathematical Society, 2006

5.5. Feller's Canonical Scale 132

5.6. Feller's Canonical Measure 136

5.7. Feller's Canonical Form 137

5.11. Classification of Boundary Points with respect to Feller's Operator 149

Niels Jacob: Pseudo-Differential Operators and Markov Processes, London: Imperial College Press

Volume 1: Fourier Analysis and Semigroups, 2001

Generators of Feller Semigroups

Volume 2: Generators and Their Potential Theory, 2002

Generators of Feller and Sub-Markovian Semigroups: Second Order Elliptic Differential Operators

Constructing Feller and Sub-Markovian Semigroups

Volume 3: Markov Processes and Applications, 2005

Feller Processes

Stochastic Integration with Jumps (Encyclopedia of Mathematics and Its Applications) - US - ISBN:9780521811293 Bichteler, Klaus / Publisher: Cambridge Univ Press, 2002/05

Feller Semigroup and Generator

Stochastic Representation of Feller Semigroups

Feller Semigroups

The Natural Extension of a Feller Semigroup

Olav Kallenberg: Foundations of Modern Probability, Springer, 2002, 2nd edition

Chapter 19. Feller Processes and Semigroups, 367-389

In July 2005 Vamsikrishna Kalapala, (B. Tech., Indian Institute of Technology, Chennai, 1998, India) defended his Master Thesis in Computer Science, entitled A Compilation of Results on Phase Transitions, Scale-Invariance [PDF] at The University of New Mexico (Albuqureque), USA. On page 2 we can read the following dedication, referring to volume 1 of Feller's Introduction to Probability Theory and Its Applications:

As we see, the dedication was written 35 years after Feller's death!

Charles M. Grinstead (Swarthmore College) and J. Laurie Snell (Dartmouth College), in their book Introduction to Probability (available online!) published by the AMS (American Mathematical Society), provide the following acknowledgments:

ACKNOWLEDGMENTS FOR FIRST EDITION
Anyone writing a probability text today owes a great debt to William Feller, who taught us all how to make probability come alive as a subject matter. If you find an example, an application, or an exercise that you really like, it probably had its origin in Feller’s classic text, An Introduction to Probability Theory and Its Applications. ...

ACKNOWLEDGMENTS FOR SECOND EDITION
The debt to William Feller has not diminished in the years between the two editions of this book. His book on probability is likely to remain the classic book in this field for many years. ...

From Tony Smith's Bounded Complex Domains:

When I was in college, Prof. William Feller said that you should always have a concrete model with which to think about abstract math structures, and that one of the most nearly universal models was the 2-dimensional Unit Disk D1 in the complex plane C1. It is a good example of a Bounded Complex Domain, whose boundary is the unit circle S1.

Here are some thoughts of Paul C. Kettler about Feller's attitude towards the division of mathematics into pure and applied (2006):

Here's another recollection of Feller. He was adamant on insisting that there is no difference between pure and applied mathematics. In his generation some departments arrogantly proclaimed that they were the "Departments of Pure Mathematics" showing overt disdain toward those who only knew "applications." Well, if he had lived longer Feller would have seen the dawning of a new golden age of mathematics (as I am certainly not the first to observe), largely and almost exclusively driven by applications. Consider algebraic K theory and string theory, or PDE advancements and the solar atmosphere, or stochastic processes and finance (my current field of interest), and on and on. Are we to consider Archimedes, Newton, Euler, and Gauss, "only" applied mathematicians because they made certain observations about flowing water, falling apples, the bridges of Königsberg, and the distributions of common things? By most accounts these are the four greatest mathematicians of history, with due respect for Euclid, Riemann, Hilbert, Einstein, and a few others.

Feller's idea (and I hope I am doing it justice here) is that there is constant reinforcement between observation and theory, and that one without the other is incomplete. Just consider how rich his widely read books on probability are in examples. He created these examples, with some assistance from his graduate students like Jay Goldman, to illustrate convincingly his points of theory. These examples were not afterthoughts, as such inclusions are in so many mathematics texts, but rather integral parts of the exposition. I challenge any to find better examples of joining theory and practice to such mutual benefit.

A quotation confirming the above discussion is the following (web site by Donald Wilson Zimmerman):

Only yesterday the practical things of today were decried as impractical, and the theories which will be practical tomorrow will always be branded as valueless games by the practical men of today.

— William Feller

Another example is 1937 Feller's review for Zentralblatt of lecture notes of Jerzy Neyman, when Feller was at the age of 31, living in Sweden:

The point of departure for the author is always actual practical problem and he never loses sight of the applications. At the same time his goal is always a truly rigorous mathematical theory. He appears to insist on absolute conceptual clarity and rigor, not only as a sound foundation, but also because it is really useful and necessary, particularly where the practical problem goes beyond the mathematical aspect...

For the Bulletin of the AMS J. Wolfowitz wrote in 1950 the following about Feller's 1950 monograph, part I:

...It is no mean feat to present so many interesting examples between two covers. They enhance the interest of the theory even for the pure mathematician, except perhaps for the extreme diehard of the "God save mathematics from its applications" school.
... To sum up, this is a superb book, and a delight to read. The gathering together of so much material in so brilliant a manner represents a prodigious amount of labor for which the mathematical public is greatly indebted. The reviewer congratulates the author; he has set a lofty standard for would-be writers of similar books to attain.

The Zagreb cemetery Mirogoj is one of the most beautiful in Europe. In order to reach the Feller family tomb, at the main entrance one has to turn to the left and proceed for about 100 meters. The Feller family tomb is considered to be one of the most beautiful pieces of art that can be seen in Arcades of the Zagreb cemetery.

The name of Vilim Feller is mentioned in a memorial tablet, among those descendants of the Feller family which were burried outside of their homeland. The name of his wife Clara Nielsen Feller is also here.

Here is the front view to the family tomb of Feller's:

Vilim Feller's mother Ida and father Eugen Viktor Feller are burried here,
together with many other relatives.

With kind permission of prof. Marta Zdenkovic, Zagreb

Ida and Eugen Viktor Feller, Vilim's parents

On the following photo you can see part of arcades of the Zagreb cemetery where the Feller family tomb is situated:

Acknowledgements.

My deep gratitude goes to Marta and Nikola Zdenkovic, Zagreb, for permission to use the photos from their family collection, and for many details about the family history. They are both grandchildren of William Feller's oldest brother Ferdinand. Many thanks to Dr. J.R. Goldman, USA, one of 17 PhD students of professor Feller, for sending me his very nice photos. Dr. Ulrich Hunger from the Universitätsarchiv Göttingen generously helped me with valuable information about Feller's doctorate. Many thanks to Paul C. Kettler, Norway, a student of professor Feller, for his kind help. I am deeply indepted to academician Sibe Mardesic, outstanding Croatian topologist, for generous help with archival and other material, and for his personal recollections about Vilim Feller, and also to his son professor Pavao Mardesic for copies of the 1964 Chinese edition of Feller's book. Professor Jozsef Pelikan from Budapest kindly sent photos of the Hungarian edition of Feller's book. Many thanks to Dr. Radmila Bulajic Manfrino, Mexico, for copies of the Spanish edition, and to Wasilio Koslow, MSc, Venezuela, for color photos. Professor John J. O'Connor from North Haugh, University of St Andrews, Scotland, kindly sent me a copy of Feller's plenary lecture in PDF (6.8 MB) form.

My dear friend Julija Vojkovic, Zagreb, helped me with her professional scanning skills. Also, my dear friend Dr. Zeljko Hanjs helped me with finding two mathematical scientific works of Feller written in Croatian, see here. Professor Branimir Dakic, Zagreb, and Mr. Tvrtko Tadic, a student of mathematics at the University of Zagreb, helped me with information about Feller's secondary schooling in Zagreb. I express my gratitude to Marta Kolar and Ines Leskovar, students at the Factulty of Electrical Engineering and Computing of the University of Zagreb, for their effort to translate the text into Croatian. Many thanks to Sinisa Milicic, University of Zagreb, for information about personal contacts between Feller and Feynman.

Errata. It has been stated by Gian Carlo Rota, MIT (Indiscrete Thaughts, Birkhäuser, 1996) that "Feller's father's surname was a "Slavic tongue twister", which William changed at the age of twenty". This is wrong, that is, the orginal second name of William Feller was always Feller, as well as for his father and grandfather. Many thanks to Marta Zdenkovic for clarifying this matter. We have noticed this mistake being spread throughout the web on numerous pages dealing with Feller. Rota's claim that the original name of William Feller was Willibrord is also wrong, the original name was Vilibald Srecko (Willibald Felix in English).

Nitis Mukhopadhyay: Probability and Statistical Inference (Statistics, a Series of Textbooks and Monographs), in the Appendix on p. 599 it is stated that "William Feller was born on July 7, 1906, in Zagreb, Yugoslavia (now Croatia)." It should be noted that Feller was not born in Yugoslavia, since it did not exist in 1906 (the ex-Yugoslavia was named so in 1929, and its predecessor had existed since 1918). In time of Feller's birth Croatia was a part of Austria-Hungary, with its own Parliament in Zagreb. For more details see here. The same mistake can be found in [Roseblatt, p 3].

We have stated at the beginning of this article that William Feller was Croatian - American mathematician. However, it would probably be more appropriate to call him Croatian - German - Danish - Swedish - American (...) mathematician. Similar is the case with many other scientists.

Request. I would deeply appreciate any additional reliable information related to the life and work of William Feller, including photos, especially if You had luck to have been his student or friend (e-mail: darko.zubrinicYYATYYgmail.com; please, remove Y's, don't ask me why).

Some of Feller's papers available online:

• Willy Feller (Stockholm): Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung, Matematische Zeitschrift, Band 40, 1935, 521-559
• W. Feller: The fundamental limit theorems in probability [PDF], Bull. Amer. Math. Soc. 51 (1945), 800-832.
• Will Feller: Review: Harald Cramer, Mathematical Methods of Statistics, [PDF], Ann. Math. Statist. Volume 18, Number 1 (1947), 136-139.
• W. Feller: On the Theory of Stochastic Processes, with Particular Reference to Applications, Proc. [First] Berkeley Symp. on Math. Statist. and Prob. (Univ. of Calif. Press, 1949), 403-432.
• William Feller and Henry P. McKean, Jr.: A diffusion equavialent to countable Markov chain, Proc Natl Acad Sci U S A. 1956 June; 42(6): 351-354.
• William Feller: Some new connections between probability and classical analysis, [PDF, 6.8 MB], plenary talk at the International Congress of Mathematicians (ICM), Edinburgh 1958, 69-86.
• William Feller, On the Equation of the Vibrating String, Indiana Univ. Math. J. 8 No. 3 (1959), 339-348 [PDF]
• William Feller, S. Orey, A Renewal Theorem, Indiana Univ. Math. J. 10 (1961), 619-624 [PDF]
• William Feller: On semi-Markov processes, Proc Natl Acad Sci U S A. 1964 April; 51(4): 653–659. [PDF]
• William Feller: On the Fourier Representation for Markov Chains and the Strong Ratio Theorem, Indiana Univ. Math. J. 15 (1966), 273-283 [PDF]
• William Feller: On the influence of natural selection on population size, Proceedings of the National Academy of Sciences, Vol. 55, 1966, 733-738
• Willim Feller: On Probabilities of Large Deviations, Proc Natl Acad Sci U S A. 1968 December; 61(4): 1224-1227 [PDF]
• William Feller: On the fluctuations of sums of independent random variables, Proc Natl Acad Sci U S A. 1969 July; 63(3): 637-639.
• William Feller: An Extension of the Law of the Iterated Logarithm to Variables without Variance, Indiana Univ. Math. J. 18 (1969), 343-355 [PDF]

Feller's papers published in

• Indiana University Mathematics Journal
• Proceedings of the National Academy of Sciences

References:

• Doob, J.L.: William Feller and twentieth century probability [PDF]. Proceedings of the Sixth Berkeley Symposium on Mathematical Statisics and Probability (Univ. California, Berkeley, Calif., 1970/1971), Vol. II: Probability theory, pp. xv-xx. Univ. California Press, Berkeley, Calif., 1972.
• Kac, M.: William Feller, in memoriam. Proceedings of the Sixth Berkeley Symposium on Mathematical Statistics and Probability (Univ. California, Berkeley, Calif., 1970/1971), Vol. II: Probability theory, pp. xxi-xxiii. Univ. California Press, Berkeley, Calif., 1972.
• William Feller, 1906-1970, Annals of Math. Statistics, 41: 6 (1970) iv-xiii (an article written jointly by Editors of the journal)
• Harald Cramer: William Feller, 1906-1970, Revue de l'Institut International de Statistique / Review of the International Statistical Institute, Vol. 38, No. 3 (1970), pp. 435-436
  This article consists of 2 page(s).
• J.W. Dauben: William Feller, American National Biography 7 (Oxford, 1999), 801-802
• J.L. Doob: Biography in Dictionary of Scientific Biography (New York 1970-1990)
• William Feller, 1907-1970, The American Statistician, Vol. 24, No. 2 (Apr., 1970), p. 42
• John Aldrich: Figures from the History of Probability and Statistics
• J.J. O'Connor and E.F. Robertson: William Feller, The MacTutor History of Mathematics archive
• Peter M. Lee: Life and Work of Statisticians, Dpt of Mathematics, The University of York, UK
• Constance Reid:
  • Courant, In Goettingen and New York, The Story of an Improbable Mathematician, Springer, 1976, see pp 111-225, 227, 247
  • Hilbert, Springer, 1996, see pp. 159, 219
• Terry Speed: Terence's Stuff: Books Worth Reading, IMS Bulletin (IMS = Institute of Mathematical Statistics), Vol 34, 2 March 2005, p 6 [local PDF]
• Nitis Mukhopadhyay: A Conversation with Ulf Grenander [PDF], Statistical Science, 2006, Vol. 21, No. 3, 404-426
• V. Vranic: Vilim Feller (1906-1970) [PDF], Ljetopis HAZU (the then JAZU) 75 (1971) 347-352 (in Croatian)
• Ulrich Krengel: Wahrscheinlichkeitstheorie, in Ein Jahrhundert Mathematik 1890-1990. Bd. 6 der Dokumente zur Geschite der Mathematik, Vieweg Verlag 1990, Braunschweig/Wiesbaden, edited by G. Fischer, F. Hirzebruch, et al., 457-459
• Glen Shaffer, Vladimir Volk: The origins and legacy of Kolmogorv's Grundbegriffe [PDF, in particular pp. 56-58], 2005 (the shorter version published as "The sources of Kolmogorov's Grundbegriffe" [pdf] in Statistical Science, Vol.21, No.1, pp.70-98, 2006.)
• Stella Fatovic-Ferencic, Jasenka Ferber-Bogdan: Ljekarnik Eugen Viktor Feller, Medicus, 1997, Vol 6, No 2, 277-283
• Sibe Mardesic:
  • Vilim Feller (in Croatian), Znanost u Hrvata: prirodoslovlje i njegova primjena, II, catalogue of exhibition at Klovicevi dvori, Zagreb, 1996
  • Neki podaci i sjecanja na profesora Fellera (Some data and recollections on professor Feller), in Istaknuti hrvatski znanstvenici u Americi (Distinguished Croatian scientists in America), Hrvatsko-americko drustvo, Matica hrvatska, Zagreb, 1997, pp. 116-121 (in Croatian and English)
• Hrvoje Sikic: William Feller, in Istaknuti hrvatski znanstvenici u Americi (Distinguished Croatian scientists in America), Zagreb, Hrvatsko-americko drustvo, Matica hrvatska, 1997 (in Croatian and English)
• Feller, Vilim (William, Willy), in Hrvatski biografski leksikon (Croatian Biographical Lexicon), Lexicographic Institute, Zagreb, 1998, Vol IV, pp 160-161 (article written by Marijana Buljan-Klaic)
• Nenad Trinajstic: The Great Men of Croatian Science (in English)
• William Feller, in Polish: William Feller urodzil sie 7 lipca 1906 roku w Zagrzebiu. W 1923 roku rozpoczyna studia uniwersyteckie, które konczy w 1925 roku z tytulem magistra. ...
• Paul R. Halmos: I want to be a Mathematician, An Automathography, Springer, 1985, pp. 94-95
• Murray Rosenblatt: William Feller 1906-1970 [PDF], Biographical Memoir, National Academy of Sciences, Washington DC, 17 pp (the year of publication is unknown to me, probably 2007, but the article seems to be much older, probably from 1970, and reedited in 2007)
• J. Wolfowitz: An introduction to probability theory and its applications, Vol. I, by William Feller, Wiley, New York, 1950, 12 + 419 pp. [PDF], BULLETIN (New Series) of the American Mathematical Society,
  Volume 37, Number 1, 1951, 109­110
• Jay Goldman: Fine Hall in the Early 60s, Pictures from Jay Goldman's Photo Album
• Mathias Feller (architect from Munich, halfbrother of Eugen Viktor Feller): Das Landhaus E.V. Feller in Agram, Innen - Dekoration, XXV. Jahrgang, Darmstadt, September 1914, 367-398
• Prva gimnazija u Zagrebu 1854.-2004., editor in chief Branimir Dakic, published by Prva gimnazija u Zagrebu, see pp 131, 194-197
• Eva Zdenkovic's letter from 1957
• Zeljko Hanjs, Darko Zubrinic: Vilim Feller (Zagreb 1906. - New York 1970.) - u povodu stote obljetnice rodjenja istaknutog hrvatsko-americkog matematicara [PDF], Matematicko-fizicki list LVII 2 (2006./2007.), 82-87
• Maja Sekulic: William Feller, Uvod u teoriju vjerojatnosti i primjene, Matematicko-fizicki list, Zagreb, No 2, 3, 4 (2007.-2008.)
• William Feller (a short summary on this web)

Zvonimir Janko, outstanding Croatian mathematician

Croatian mathematical diaspora

Croatian Science

Croatia - History, Culture and Science