

|
Professor Zvonimir Janko, Mathematical
Institute, University of Heidelberg, Germany, at the University of
Zagreb, Faculty of Electrical Engineering and Computing, November 26,
2007, at a scientific meeting organised on the occasion of his 75th
birthday by his students and collaborators in Croatia.
|
|
Contents of this web page |
Classification TheoremLet us state the famous Classification Theorem for finite simple groups.
Definition of the group, with a few examples and applications. More advanced, for beginning graduates: J.S. Milne, Group Theory, 2007, 121 pp. Daniel Gorenstein, the first person to put forward a plan for classifying all the finite simple groups, started the introduction to his book "The Classification of Finite Simple Groups" with the following words:
A few pages later Gorenstein continues: It is therefore not surprising that the Classification theorem, the formulation of which is rather short, is also called enormous theorem due to its enormously long proof. Moreover, there is not a single expert capable to understand the proof of the Classification Theorem in its entirity. |

|
Professor Zvonimir Janko delivered an
invited lecture about his results concerning sporadic groups at the
International Congress of Mathematicians in Nice, France,
in 1970. Behind him on the right is professor Vladimir Devidé,
University
of Zagreb,
his
PhD
advisor.
|
Janko groupsThe sporadic groups have been discovered already in the 19th century by Émile Léonard Mathieu (1835-1890). Mathieu goups M11 and M12 have been discovered in 1861, and M22, M23, and M24 in 1873. It took more than 90 years after the discovery of the last Mathieu group (and more than a century after the discovery of the first Mathieu group) until professor Zvonimir Janko, then a young mathematician at the age of 32, constructed a new sporadic group in 1964, now called J1 in his honour. It has 175,650 elements. Professor Zvonimir Janko in 1964, at the age of 32, when he discovered J1 The discovery of J1 in 1964 (published in 1966) was a tremendous surprise in mathematical community. It had been "received as a sensation by the specialists in group theory", see [Held, p1]. This discovery has launched a modern theory of sporadic groups. Zvonimir Janko at that time worked in Australia, at The Australian National University (his name is included within Notable past staff) in Canberra, capital of Australia. Subsequently Janko discovered three more sporadic groups:
In 1967 Higman and Sims constructed sporadic group HS. John Conway constructed three sporadic groups, Co1 and Co2 in 1968, and Co3 in 1968. Dieter Held constructed a sporadic group now called He (with G. Higman and Mc Kay), J.E. McLaughlin and Michio Suzuki constructed respective sporadic groups Mc and Su in 1968. Fischer constructed groups M(22), M(23) and M(24)' in 1969. Richard Lyons and Charles Sims constructed Ly in 1970, Rudvalis, Conway and Wales constructed Ru in 1972. The same year Michael O'Nan and Charles Sims discovered ON. In 1974 the following three sporadic groups have been discovered: F5 by John Thompson and Stephen Smith, F3 by Koichiro Harada, Simon Norton and Scmith, and F1 by Bernd Fischer and Robert Griess. The sporadic group F1 is the largest one, better known as the Monster group. It has approximately 8x1053 elements, or precisely 808,017,424,794,512,875,886,459,904,961,710,757,005,754,368,000,000,000 elements. The second largest one is F2, called the baby Monster, which has4,154,781,481,226,426,191,177,580,544,000,000 elements. The fourth largest sporadic group is J4, with order equal to 86,775,571,046,077,562,880 It should be stressed that Zvonimir Janko not only discovered the first sporadic group in the 20th century (J1 in 1964), but also the last one (J4 in 1975). So Janko somehow opened and closed the quest for all sporadic groups in the 20th century. It resulted in the discovery of altogether 21 sporadic groups in the 20th century. The fascinating quest for new sporadic groups has resulted, besides four Janko groups, in the discovery of 17 of them in the period from 1967 to 1975: one jointly by Donald Higman and Charles Sims; one each by Dieter Held, Richard Lyons, Jack McLaughlin, Michael O'Nan, Michio Suzuki, and Arunas Rudvalis; three by John Conway; and seven by Bernd Fischer, with important contributions by Robert Griess. The largest one, discovered by Fisher and Griess, is well known as The Monster. In 1981 it has been proved by Simon Norton, Cambridge University, that there are no other sporadic groups than these 26 peculiar groups. In January 1981 M. Aschbacher declared during a solemn session of the American Academy of Sciences that all finite simple groups are known. This meant that the Classification Theorem has been proved, and Janko's contribution to its proof was enormous. However, it turned out that Aschbacher's announcement was premature, since many mistakes have been found in the studies of the so called quasi-thin groups, and this has been finally settled in 1992, see Janko's survey paper [Janko], p 179. The name of "sporadic groups" has been introduced by William Burnside in his monograph Theory of Groups of Finite Order, 1911, in which he indicated an exceptional nature of Mathieu groups: "These apparently sporadic simple groups would probably repay a closer examination than they have yet received." In this way he forsaw the avalanche of investigations which ensued only after 1964, when Janko discovered his J1. To illustrate the "earthquake" in group theory which raised Janko's discovery of J1 we cite the following testimony from [Ćepulić] (translated from Croatian by D.Ž.). In 1997, during the celebration of 65th birthday of professor Janko in Mainz, Bertram Huppert, the author and coauthor (with Norman Blackburn) of the most extensive, encyclopaedic treatise and manual on finite groups, Endliche gruppen I, II, III, said roughly the following: "There were a very few things that surprised me in my life. I experienced the Second World War. It could have been predicted that there will be war. I believe it will surprise you, and some of you may be shocked by what I am going to say. There were only the following two events that really surprised me: the discovery of the first Janko group and the fall of the Berlin Wall." Professor Vladimir Ćepulić from the University of Zagreb was a witness of the following interesting event in Göttingen, which nicely illustrates the importance of this discovery. In his investigation professor Janko exploited modular characters of groups, a theory developed in 40s and 50s of the 20th century by Richard Brauer, one of the most famous mathematicians. Professor Richard Brauer, a German emigree to the USA, was a visiting professor in the academic year 1964/65 at the Mathematical Institute in Göttingen, where I also participated as a stipendist of the Humboldt Foundation, and attended his lectures. Professor Brauer arrived to his first lecture after Christmas visibly excited, carring a piece of paper in his hand and saying: "I have received this mail from Zvonimir Janko from Australia, in which he informs me that using my theory of modular characters he found a new sporadic finite simple group!" ([Ćepulić], translated form Croatian by D.Ž.) The name of Zvonimir Janko has been included twice into the Encyclopaedia Britannica Year Book with extensive presentations of his work written by Irving Kaplansky, a famous algebraist. See [Devidé]. |

Hall-Janko graph, source en.wikipedia.org,
(there are 90 outer vertices and 10 inner vertices)
|
Group J2 has 604 800 elements. It is the only one among four Janko groups to be a subgroup of the Monster. Therefore, it makes part of the so called "happy familly", a name coined by Robert Griess, see here. The "happy familly" is defined as the set of all sporadic groups that are proper subgroups of the Monster. There are 20 such groups. So, there are five groups which do not belong to the "happy family", and three of them are the Janko groups: J1, J3, andJ4. As we see, 26 sporadic groups are in some sense "exceptional" groups, and furthermore, the three indicated Janko groups are in some sense "exceptional" among sporadic groups! Unlike the Fischer groups, Conway groups, and Mathieu groups, the Janko groups do not form a series and have little in common, see here. In the construction of the Janko group J1 for the first time a computer in Canberra has been used in algebraic studies. This was the first Australian scientific computer. The group J1 has found applications in the physics of elementary particles. With the discovery of J1 Janko showed that a claim due to R. Brauer and J. Thompson about nonexistence of new simple groups was wrong (see Janko's biography in [Croatian biographical lexicon], p 323. Janko describes in his lively article [Janko, pp 176-177] how thanks to encouragement of his wife Zora to be persistent, he managed to find mistakes in the works of Thompson and Brauer. And these mistakes of great mathematicians brought him to discovery of J1 in 1964. That is why he calls J1 also Zora's group (Zorina grupa in Croatian, see in [Hanjs]), in honour to his wife. At that time Janko was a research fellow in Canberra, and this discovery immediately brought him the position of full professor at the University of Monach in Melbourne in 1965 at the age of 33, which meant that he skipped the usual three academic steps. The group J2 has several geometric realizations, and according to his own words, see [Janko, p 177], the most beautiful is the one found by Jacques Tits from Paris. After eight years of thorough investigations Janko managed to discover the group J4. It was discovered in Heidelberg, in May 21st, 1975, using the famous Thompson formula, and without any help of a computer (becuase it is impossible), see Janko's survey article [Janko, p 179]. Paul Halmos (1916-2006) in his well known book I have a photographic memory (Providence, 1987) provides photos of many outstanding mathematicians. Two of them are from Croatia: Zvonimir Janko and William Feller.
|

Professor Janko is an aggreable and communicative person.
Simple groups balladBelieve it or not, Janko's groups have entered a ballad! Here is A Simple Ballad dealing with simple groups, due to anonymous author, and published by the American Mathematical Monthly, Nov. 1973 (provided on the web by Hubert Grassmann).
Remark 1. Found scrawled on a library table in Eckhart Library at the U. of Chicago; author unknown or in hiding. (See W. E. Mientka, Professor Leo Moser - Reflections of a Visit, American Mathematical Monthly 79 (1972), 609-614.) Remark 2. The ballad was written before the discovery of the last sporadic group in 1975, that is, of the Janko group J4. In other words, the ballad is far from being finished. |
Orders of all 26 sporadic simple groups, from the David Madore web page:
(spor-m11) |
7920 |
(spor-m12) |
95040 |
(spor-j1) |
175560 |
(spor-m22) |
443520 |
(spor-j2) |
604800 |
(spor-m23) |
10200960 |
(spor-hs) |
44352000 |
(spor-j3) |
50232960 |
(spor-m24) |
244823040 |
(spor-mc) |
898128000 |
(spor-he) |
4030387200 |
(spor-ru) |
145926144000 |
(spor-sz) |
448345497600 |
(spor-on) |
460815505920 |
(spor-co3) |
495766656000 |
(spor-co2) |
42305421312000 |
(spor-f22) |
64561751654400 |
(spor-f5) |
273030912000000 |
(spor-ly) |
51765179004000000 |
(spor-f3) |
90745943887872000 |
(spor-f23) |
4089470473293004800 |
(spor-co1) |
4157776806543360000 |
(spor-j4) |
86775571046077562880 |
(spor-f24) |
1255205709190661721292800 |
(spor-f2) |
4154781481226426191177580544000000 |
(spor-f1) |
808017424794512875886459904961710757005754368000000000 |

How was J1 discovered?
DescendantsAccording to Mathematical Geneaology Project, the following eighteen mathematicians are PhD students of professor Zvonimir Janko, and he has 83 descendants (as of 2022):
In fact, the number of his scientific descendants, direct and indirect, is much larger. In Croatia only there are about 20 of them.
|

Professor Zvonimir Janko is a member of Advisory
Board of Glasnik
Matematički,
a scientific journal issued by the Croatian Mathematical Society.

| Professor Zvonimir Janko is a corresponding memberof the Croatian Academy of Sciences and Arts since 1995. He is a member of the Heidelberg Academy of Sciences since 1972. In 1970 the French Academy of Sciences decorated him with a medal for the discovery of his sporadic groups. Since 1998 he is a honorary citizen of Bjelovar, his native town. |
|
In May 24, 2006, the following lecture was delivered at the Lighthill Institute of Mathematical Sciences in London: SYMMETRY AND THE MONSTER This talk will describe the quest to find a complete list of all finite simple groups. These groups, the basic building blocks for all finite groups, were instrumental in Galois' work on the solvability of algebraic equations; and he himself discovered some important ones. More were exhibited in Jordan's great treatise in 1870, and further families emerged from Lie's work, as a result of the classification work by Killing and Cartan in the late nineteenth century. After the Second World War new families of simple groups were discovered, and there was enormous interest in finding a complete list. A way forward was found using work of Richard Brauer, and the great theorem of Walter Feit and John Thompson. They showed that every finite simple group whose order is not a prime number must contain elements of order 2, leading to some important subgroups that offered a method for completing the list. To cut a long story short, while Thompson was advancing these new methods, Zvonimir Janko, a Croatian mathematician working in Australia, surprised the world with a very strange exceptional group. This was the first exception since Émile Mathieu discovered five beautiful groups of permutations in the nineteenth century, and it really set the cat among the pigeons. Further new exceptions came thick and fast, and they were dubbed "sporadic groups". The largest is called the Monster. This talk will explain how the Monster was discovered, and how it came to reveal strange connections between number theory and mathematical physics, sometimes called the moonshine connections. Marc Ronan: Symmetry and the Monster, One of the Greatest Quests of Mathematics, Oxford University Press, 2006 (mathematicians involved in this book, including professor Janko): from the book review [PDF] by Robert L. Griess published in the Notices of the American Mathematical Society, February 2002: ... Zvonimir Janko, like Fischer, had very strong personal ideas about where to look for new simple groups, and he worked them quite hard. Janko's most successful theme was the so-called "O 2 extraspecial" hypothesis for centralizers of involutions. The flavor of Janko's program was more "internal group theory" rather than "external geometry". Fischer and Janko each found several new sporadic groups but by mining rather different parts of the group theory terrain. ...
|

Professor Zvonimir Janko with his wife Zora.
A short biography of Zvonimir JankoProfessor Zvonimir Janko was born in Bjelovar, Croatia, in 1932. He studied mathematics at the University of Zagreb. After graduation he was sent to work at a high school in a small town of Lištica (also known as Široki Brijeg - Wide Hill) in Bosnia and Herzegovina, where he was teaching physics. There he had already started to publish his first scientific works. It is at that time that he learned about groups, and found it interesting that only four axioms in the definition are the starting point of enormous theory. It is amusing that he was receiving letters from editorial boards indicating "University of Listica" in his address! And the highest educational institution in the town was the high school where he worked. Professor Janko's wife Zora is from Lištica. He earned his PhD at the University of Zagreb in 1960 under (formal) supervision of professor Vladimir Devidé. The title of the thesis was Dekompozicija nekih klasa nedegeneriranih Rédeiovih grupa na Schreierova proširenja (Decomposition of some classes of nondegenerate Rédei Groups on Schreier extensions), in which he solved a problem proposed by an oustanding Hungarian mathematician Laszlo Rédei. Professor Stanko Bilinski (PDF) was the head of the PhD exam committee. Until 1962 Janko alreday had about ten published journal articles, thus satisfying conditions for the position of assistant professor of mathematics at the University of Zagreb. Despite excellent results of a young talented mathematician, Janko was not able to find an adequate job in the communist Yugoslavia. His only "fault" was his particiaption in students' visit to the grave of the 19th century Croatian politician Dr. Ante Starčević, for which he was draconcially punished by two years of suspension of his studies. This is why his studies were prolonged for two years, from 1950 til 1960. He applied thirteen times for the position of Research Fellow or Assistent Professor in ex-Yugoslavia, but in vain (even in Tuzla in Bosnia and Herzgovina.) Therefore Janko decided to go to Australia, where he spent seven years, 1962-1968. He was first employed at the Australian National University in Canberra where he stayed until 1964, and then after his discovery of J1 obtained a position of full professor at Monash University in Melbourne, skipping the usual three academic steps. He then moved to the USA, where he spent the period of 1968-1972 first as a visiting professor in Princeton, and then as a full professor at the Ohio State University in Columbus. Since 1972 until his retirement in 2000 Janko was a full professor at the University of Heidelberg, Germany. But even after his retirement his scientific activity is still amazing. His work can be roughly divided into three parts:
Professor Janko is a great fan of theatre and a passionate chess player. In 2007, when he celebrated 75th birthday, his father celebrated 100th brithday in Bjelovar singinig and playing violin. Here we reproduce a very short, but significant biographical sketch written by professor Zovnimir Janko himself, on the occasion of his very much belated admission to the Croatian Academy of Sciences and Arts in 1993. His admission was not possible ex- Yugoslavia. The biography was written in Croatian language, and published in the Notices of the Croatian Academy of Sciences (Vjesnik Hrvatske akademije znanosti i umjetnosti), see [Janko, p 180].
Professor Janko delivered a lecture at the Croatian Academy of Sciences and Arts in Croatian, entitled "Kako sam pronašao četiri sporadične grupe" (How I discovered four sporadic groups), March 24th, 1993, published with the above biographical sketch in [Janko].
Source: [Šiftar] Sažetak Zvonimir Janko (Bjelovar 1932.), znameniti je matematičar. Osnovnu školu i gimnaziju pohađao je u Bjelovaru. Studirao je matematiku u Zagrebu, gdje je diplomirao (1956.) i doktorirao (1960). Nakon diplome radio je u Širokom Brijegu (tada Lištica) u Bosni i Hercegovini. Razdoblje 1962. - 1968. proveo je u Australiji, najprije u Canberri (1962 - 64.), a zatim kao redoviti profesor na Monash University u Melbourneu (1965.-68.). Od 1968. do 1972. Janko je proveo u SAD kao gostujući profesor na sveučilištu Princeton a potom kao redoviti profesor na Ohio State University u Columbusu (Ohio). Od 1972. do umirovljenja (2000.) redoviti je profesor Sveučilišta u Heidelbergu (Njemačka). Z. Janko je poznat po dostignuća iz matematičke discipline teorije konačnih grupa. Najznačajnija su mu otkrića novih sporadičnih prostih grupa, danas poznatim pod nazivom Jankove grupe. Ostavio je neizbrisiv trag i u teoriji projektivnih ravnina i dizajna. Profesor Zvonimir Janko sudjelovao je u poslijediplomskoj nastavi na Matematičkom odjelu Prirodoslovno-matematičkog fakulteta u Zagrebu, održao je niz predavanja u Zagrebu, Splitu i Mostaru. Suradnik je i mentor mnogim hrvatskim i stranim matematičarima. Dopisni je član Hrvatske akademije znanosti i umjetnosti. Tijekom rada u Heidelbergu zapažena je njegova pomoć Hrvatskoj u različitim oblicima.
|

Professor Zvonimir Janko had 18 students,
who earned ther PhD titles in the fields of group theory and finite
geometries.
He has 83 descendants (as of 2022), see his Mathematical
Geneaology.

The audience in full concentration...

Professor Goran Muić belongs to younger generation of Croatian top mathematicians.
Monographs dealing with Janko groupsMichael Achbacher, Sporadic Groups, Cambridge Tracts in Mathematics, 104, 1994
Chapter 16. Groups of Conway, Suzuki, and Hall-Janko type Daniel Gorenstein:
Cheryl E. Praeger, Leonard H. Soicher: Low Rank Representations and Graphs for Sporadic Groups, Australian Mathematical Society Lecture Series, Cambridge University Press, 1997. The book contains six sections dealing with Janko groups:
Robert Griess, Twelve Sporadic Groups, Springer monographs in Mathematics, Springer, 1998 Chapter 10: Subgroupsw of Conway Groups; the Simple Groups of Higman-Sims, McLaughlin, Hall-Janko and Suzuki Book Description Robert Griess: Wandering About Sporadic Groups (Colloquium organized in 2019 at the State University in Sankt Peterburg, Russian Federation) In this video, at 28:25, Professor Griess (answering a question from the audience), claims that it is still not known if the class of sporadic groups is finite. In particular, the Classification "Theorem" is still not proved. (DŽ)A.A. Ivanov: The Forth Janko Group, Oxford Mathematical Monographs, 2004, 250 pp Alexandar Antolievic Ivanov is professor of pure mathematics at Imperial College, London, trained as a mathematician in Moscow, Russia
The title of the book on the front conver is simply J4 :
And the inside title reveals to full title of Ivanov's monograph:
Gerhard Michler: Theory of Finite Simple Groups, Cambridge University Press, 2006 Section 8.5: Janko's sporadic groups, pp. 409-418 Chapter 9: Janko group J1, pp 433-454
|

|
Professor Vladimir Volenec, behind him
professor Goran
Muić, dean of the Department of Mathematics of the University of
Zagreb, in the next row professor Mario Essert.
|

Formulation of the Classification Theorem for finite simple groups in Croatian.

|
Professor Vladimir Ćepulić, delivering an
opening lecture on the work of Zvonimir
Janko in group theory, and discussing the Classification Theorem
for finite simple groups.
|

|
Professor Vladimir Ćepulić delivering his lecture about Janko's work in group theory;
Janko in the front row. V. Ćepulić is a specialist in group theory, and
a PhD
student of Dieter
Held.
|

Elizabeta Kovač-Striko, Zvonimir Janko, Vladimir Ćepulić (lecturer), and Zora Janko

Professor Vladimir Ćepulić

Ready for the next lecture to be delivered by...

Professor Juraj Šiftar, University of Zagreb, a student of professor Janko.

Professors Juraj Šiftar and Mario-Osvin Pavčević, two generations of professor Janko's students.

Professor Mario-Osvin Pavčević opening the scientific meeting

|
Professor Goran Muić, dean of the Department
of Mathematics of the University of Zagreb, in his address in honour of
professor Zvonimir Janko.
|
|
Sporadic Groups In the mid-to-late nineteenth century, the French mathematician Émile Mathieu created five very exceptional groups of permutations, the largest of which is called M24. Mathieu's groups did not fit into the later periodic table, and remained the only exceptions for a hundred years, until the Croatian mathematician, Zvonimir Janko found a new one that he published in 1966. This inspired the search for other sporadic groups, and their discovery is an intriguing story involving a variety of methods: some geometric, some involving patterns exhibiting interesting permutations, and some by analyzing possible cross-sections (called 'involution centralizers' in group theory). These latter cases were very technical, and the construction of the sporadic group was a tricky business, usually involving computer techniques. The Monster - the largest sporadic group - was predicted by the cross-section method, but its size and complicated structure rendered computer methods impractical, and it had to be constructed by hand. There are two main threads that led to the Monster. One was the Leech Lattice and the Conway groups. Source: The Whole Story by Mark Ronan Invariant Society, The Student Mathematical Society of the University of Oxford Prof. Mark Ronan, University of Illinois,
Visiting Professor at UCL This talk will describe the quest to find a complete list of all finite simple groups. These groups, the basic building blocks for all finite groups, were instrumental in Galois' work on the solvability of algebraic equations; and he himself discovered some important ones. After the Second World War new families of simple groups were discovered, and there was enormous interest in finding a complete list. Whilst this was going on, however, Zvonimir Janko, a Croatian mathematician working in Australia, surprised the world with a very strange exceptional group. This was the first exception since Émile Mathieu discovered five beautiful groups of permutations in the nineteenth century, and it really set the cat among the pigeons. Further new exceptions came thick and fast, and they were dubbed "sporadic groups". The largest is called the Monster. This talk will explain how the Monster was discovered, and how it came to reveal strange connections between number theory and mathematical physics, sometimes called the moonshine connections.
|

|
Professor Mario-Osvin Pavčević, University of Zagreb, one of the organizers of the meeting on the occasion of 75th birthday of professro Janko. |

|
Professor Zvonimir Janko in friendly discussion with two generations of his indirect students: Professor Vladimir Ćepulić (University of Zagreb) and dr. Sanja Rukavina (University of Rijeka). |

Some of the activities related to the work of Zvonimir JankoThe number n of involutions in a finite 2-group G is odd. If n=1, then it is known for already 200 years (and available in any textbook on algebra) that then the group G is either cyclic or a generalised quaternionic group. However, the case of of n=3 is surprisingly difficult, but exceptionally important in the theory of finite groups. Despite some attempts to solve this problem (A.D.Ustjuzaninov in 1972 and M. Konviser 1973), it was only in 2004 that due to results of Zvonimir Janko the 2-groups G with n=3 have been satisfactorily classified. Professor Janko delivered a lecture in November 11th, 2007 about his results at the Scientific Colloquium of the Croatian Mathematical Society, entitled: Rjesenje problema tri involucije (A solution of the problem of three involutions). Broj involucija n u konačnoj 2-grupi G je neparan. Ako je n=1, tada je poznato već 200 godina (i nalazi se u svakom udžbeniku algebre) da je grupa G ciklička ili generalizirana kvaternionska grupa. Međutim, sljedeći slučaj n=3 je začuđujuće težak, ali izrazito važan za teoriju konačnih grupa. Mada je bilo pokušaja, da se taj problem riješi (A.D.Ustjuzaninov 1972. i M.Konviser 1973.), tek su ovogodišnjim rezultatima Zvonimira Janka 2-grupe G s n=3 klasificirane na zadovoljavajući način. In May 26, 2004, at the Colloquium of the Rudjer Boskovic Institute in Zagreb, professor Janko delivered a lecture entitled Moderna teorija konačnih p-grupa (Modern theory of finite p-groups). February 14, 2005, Colloquium at the Freie Universität Berlin, Germany Barbara Baumeister -Freie Universität Berlin The third group of JankoAbstract: In an enormous proof all the finite simple groups have been classified. (Recall that a group is simple if it has no normal subgroup other than 1 and G.) There are some infinite families and 26 sporadic exceptions. One of them is specially difficult to handle, the third group of Janko, J3. Janko gave evidence that there is a simple group G satisfying the two conditions:
Such a group is called "group of J3-type". He also showed that a group of J3-type has 50.232.960 elements. In my PhD thesis I proved the existence of a group of J3-type by constructing a geometry with automorphism group isomorphic to J3. Using this information I am now trying to show that there is just one group of J3-type up to isomorphism. 13th British Combinatorial Conference, University of Surrey, Guildford, 8-12 July 1991 ... one of contributed talks: M. Weidenfeld, A construction for the graph associated with the small Janko group Algebra Research Group, Oxford November 20, 2001, Dr. M. Holloway Oxford, Miles Holloway: Broue's conjecture for the Hall-Janko group and its double cover. Proc. London Math. Soc. (3), 86(1):109-130, 2003. Université Libre de Bruxelles, Département de Mathématique 1996, D. Leemans: Department of Mathematical Sciences Binghamton University, State University of New York The Algebra Seminar, 2007 October 16: Hyun Kyu Kim (Cornell) University of Birmingham, School of Mathematics Pure Maths Research Staff & Activities, 2007 Finite Classical and Sporadic Groups (Professor Rob Curtis, Professor Chris Parker, Professor Sergey Shpectorov, Dr Corneliu Hoffman, Dr Yongzhong Sun, Emeritus Professor J Wilson) ... Curtis has provided fresh insight into the Mathieu groups and done a lot to explain the existence of other sporadic groups. His approach yields presentations and constructions of these groups which reflect their geometry and symmetry and which are easy to work with. His techniques have recently yielded an elementary proof of the existence of the smallest Janko group. Additionally, the largest Janko group and the Conway group .O have been constructed from this point of view. This approach also reveals remarkably analogous constructions for the Held group and the Harada-Norton groups, which are respectively centralizers of an element of order 7 and an element of order 5 in the Monster. One of his goals is to find a uniform method for the construction of these exceptional and remarkable structures and together with Parker he has had funding from the EPSRC for this purpose. ... Representation Theory, General Finite Groups and Associated Geometries (Professor R Curtis, Professor CW Parker, Dr PJ Flavell, Dr AD Gardiner, Dr Corneliu Hoffman, Dr I Korchagina) ... Professor Rob Curtis, in collaboration with Dr John Bray, has produced an effective double coset enumeration procedure for symmetrically presented groups; this program has been implemented by the latter researcher and works well for large groups, including the largest Janko group J4. The classification of the finite simple groups requires about 15,000 journal pages. Many mathematicians world-wide are trying to give new and better proof for results needed in the classification. Dr Inna Korchagina works jointly with Professors Ron Solomon and Richard Lyons, the two people most heavily involved in producing the definitive classification of finite simple groups after the untimely death of Daniel Gorenstein. Her recent work characterizes simple groups such as the Suzuki and Thompson groups which have mixed characteristics. Robert Curtis: Symmetric Generation of Groups: With Applications to many of the Sporadic Finite Simple Groups (Encyclopedia of Mathematics and its Applications), Cambridge University Press, 2007, 332 pp Book Description About the Author |

|
Professor Zvonimir Janko with professor Elizabeta Kovač-Striko, University of Zagreb, on the right, also his PhD his student. |

|
Dr. Tanja Vučičić and Dr. Snježana Braić, students of professor Zvonimiro Janko from the University of Split. |
Finite Geometries and Design TheoryProfessor Zvonimir Janko worked in this fields in the period of 1980-2000. Among his close collaborators we mention Tran van Trung, Vladimir Tonchev, and Hadi Kharagani. In 1987 he delivered a minicourse at the Mathematics Department in Zagreb, consisting of five lectures under the common title Design Theory. |
Groups of Prime Power OrderYakov Berkovich, a Russian mathematician now working at the University of Haifa, Israel (address: Department of Mathematics, University of Haifa, Mount Carmel, Haifa 31905, Israel), has a very fruitful collaboration with Zvonimir Janko in the past years. He is preparing a monograph entitled "Groups of Prime Power Order", which was originally planned to be issued in 2001. However, Zvonimir Janko has obtained so many substantially new results that Berkovich postponed issuing the book, since otherwise the book would be immedately outdated. Moreover, professor Berkovich claimed in 2001 that some of the results that Janko had recently obtained in this field are the most important in the past 30 years! Meanwhile, the material has grown enormously, and now the monograph will be issued in three parts, starting with 2008. The second and third part will be a joint work of professors Berkovich and Janko. Saunders MacLane placed Zvonimir Janko among originators of the theory of p-groups.
A voluminous hardcover monogrpah issued in 2008, 520 pp. Vol 2, Vol 3, Vol 4, Vol 5, and Berkovich, Yakov G.; Janko, Zvonimir Groups of prime power order. Vol. 6. De Gruyter Expositions in Mathematics, 65. De Gruyter, Berlin, 2018. xxi+385 pp. For more information see MathSciNet.
|

Professor Zvonimir Janko at the University of Zagreb, 2007
A lecture by professor Zvonimir Janko
in Zagreb in June 2017
On June 2nd, 2017, Professor Zvonimir Janko visited the
Faculty of Electrical Engineering and Computing of the University of
Zagreb in order to delivered a lecture entitled "Čudno ponašanje
konačnih p-grupa" (in
Croatian, Strange behavior of p-groups),
organized within the Seminar for finite geometries and groups. The
seminar has been opened by one of its leaders, Professor Mario Osvin
Pavčević. The talk has raised a great interest, so that some colleagues
from the Universities of Split and Rijeka arrived to Zagreb especially
for that occasion. |


Professor Zvonimir Janko with Professors Tanja Vučičić and Anka
Golemac,
his colleages from the University of Split.

Professor Zvonimir Janko, Univeristy of Heidelberg, with Professors
Ljubo Marangunić
and Zijad Haznadar, University of Zagreb.

Professor Mario Osvin Pavčević opening opening the seminar with the
talk of
Academician Zvonimir Janko, organized at the University of Zagreb on
June 2nd, 2017.

Profeesor Zvonimir Janko starting his talk "Čudno ponašanje konačnih p-grupa"
(in Croatian, Strange behavior of p-groups)
Nine photos that follow have been
provided by Professor Ljiljana Bralić from the University of Split:


Zvonimir Janko with Anka Golemac, professor at the University of Split

Professor Zvonimir Janko is an agreable and communicative person.


Answering questions

Jankova otkrića potresla su matematičke znanstvenike u
svijetu (interview, in Croatian)
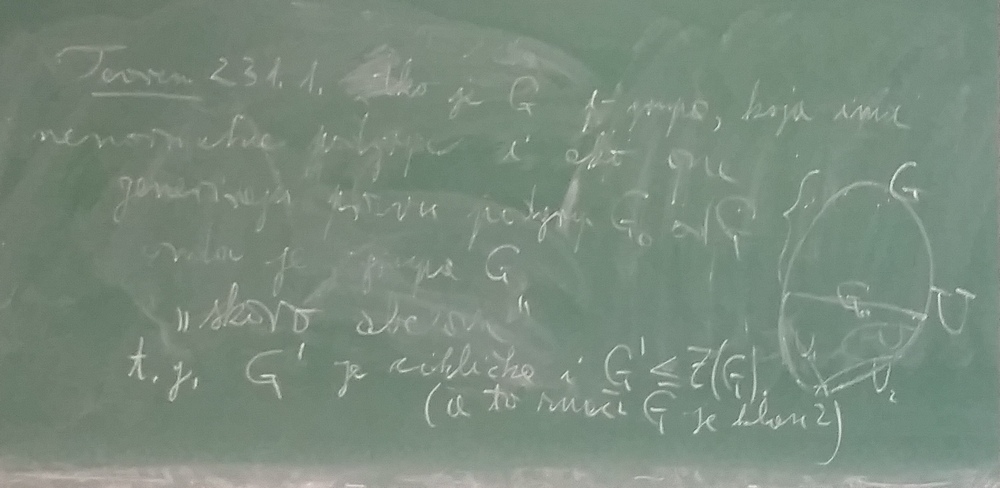
Theorem 231.1, formulated in Croatian

Professors Snježana Braić of the University of Split and Sanja Rukavina
of the University of Rijeka.

Professors Anka Golemac, Zvonimir Janko and Tanja Vučičić.
Many thanks to Professor Ljiljana
Bralić, University of Split, for providing the above 9 photos.
Collaboration with Croatian mathematiciansIn winter semester of 2000 Janko taught a postgraduate course Finite Groups Theory (30 hours) at the University of Zagreb, Department of Mathematics, PMF. In the years of 2000-2003 professor Janko delivered courses for graduate students at the Department of Mathematics, University of Zagreb, in which he introduced listeners into the field of his current research - the theory of finite p-gourps. The lectures were delivered in his characteristic way - clearly and precisely, and at the same time with a lots of humour. He taught from the very beginning, lecturing elements of group theory, till contemporary probelms of current investigations. See [Ćepulić]. He had numerous lectures in group theory and design theory, and his students work in Zagreb, Rijeka and Split (in Croatia), and in Mostar (in Bosnia and Herzegovina). He supervised many PhD theses in Croatia. Dr. Zdravka Božikov, University of Split, was among the first Croatian mathematicians to earn her PhD thesis (1984) under the guidance of professor Janko. Zvonimir Janko has many collaborators, not only in Croatia, so that one can speak about Janko's School, see [Šiftar]. In 2007 professor Janko obtained a special recognition from two German institutions, German Rector's Conference and German Research Foundation (Deutsche Forschungsgemeinschaft, DFG), for his contribution to the development of mathematics research in South East Europe. His students are in Croatia, Bosnia and Herzegovina, and Kosovo, see [Ćepulić].
THE INSTITUTE OF
COMBINATORICS AND ITS APPLICATIONS written by Professors Dean Crnković (University of Rijeka) and Mario Osvin Pavčević (University of Zagreb) In 1998, Professor Zvonimir Janko was proclaimed a honorary citizen of his native city of Bjelovar.  Professor Zvonimir Janko, Source - Zavičajna zbirka Bjelovar. Selected articles kept at Zavičajna zbirka (Regional Collection) Bjelovar.
Professor Zvonimir Janko in the 21st century. Source of the photo Wikipedia.  Professor Zvonimir Janko in 1986. Source Bjelovarski list.  In 1991, professor Zvonimir Janko (on the far right) helped in establishing academic collaboration between Universities of Heidelberg and Zagreb. Next to him, Professor Osman Muftić, Minister of Science of the Republic of Croatia. On the left, colleagues from the University of Heidelberg. Photo taken at the University of Heidelberg, published by the Heidelberger Nachrichten.
|
Mathematical notions bearing the name of Janko
|
References related to Janko groupsSource: Ben Fairbairn, University of Birmingham, Sporadic Group References Janko group J1
Hall-Janko group J2/HJ
Janko group J3
Janko group J4
|
|
Literature
Lectures (videos) Robert
Griess: My life and times with the sporadic simple groups
Robert Griess: Wandering About Sporadic Groups John Conway: The Monster Group Monster Group (John Conway) - Numberphile Richard E. Borcherds: Sporadic groups and number theory Richard
Borcherds: Sporadic Groups - The Archimedeans Simple
Groups - Abstract Algebra 10,000
page proof! The Classification of Finite Simple Groups Simple groups, Lie groups, and the search for symmetry II | Math History | NJ Wildberger
|
|
Acknowledgements. Many thanks to professor Zvonimir Janko for kindly providing his 1964 photo upon my request. I express my deep gratitude to professor Vladimir Ćepulić, University of Zagreb, for his illuminating article dealing with life and work of professor Zvonimir Janko. Photos from the 2007 conference held in honour of professor Janko which are of the form janko_m*.jpg are shot by professor Mario Pavčević, janko_k*.jpg are by Kristijan Tabak, M.Sc, janko_s*.jpg by Siniša Miličić, dipl.ing., and the rest is by Darko Žubrinić, the author of this web page. |
William Feller, distinguished Croatian - American mathematician
Alex Grossmann, distinguished Croatian-French
physicist and mathematician,
a founder of Wavelet Theory