Gustoća Lissajousovih krivulja

Krunoslav Popović
I. gimnazija Varaždin u Varaždinu
e-mail: krunopopovic@yahoo.com

Uvod

Na internetu ima puno zanimljivih tema iz računalne grafike. Jedna od njih su Lissajousove krivulje (čitaj Lisažuove, s naglaskom na u). One se pojavljuju i u elektrotehnici kod tzv. osciloskopskih mjerenja. Ako su $m$, $n\in\mathbb{N}$, prirodni brojevi, Lissajousova krivulja se zadaje parametarski ovako:
$$
x=\cos mt, y=\sin nt, \quad t\in\mathbb{R}
$$To znači da točka $T(\cos mt,\sin nt)$ crta Lissajousovu krivulju kada broj $t$ prolazi skupom $\mathbb{R}$ realnih brojeva.

Istu Lissajousovu krivulju možemo zadati s više parova brojeva $m$ i $n$. Na pr. s $x=\cos2t$, $y=\sin3t$ zadana je ista krivulja kao s $x=\cos(2\cdot2t)$, $y=\sin(3\cdot2t)$, jer kada broj $t$ prolazi skupom $\mathbb{R}$, onda i broj $2t$ prolazi cijelim skupom $\mathbb{R}$. Mi ćemo kasnije proširiti pojam Lissajousove krivulje na realne brojeve $m$, $n\in\mathbb{N}$.

Ako su $m$, $n\in\mathbb{N}$, lako se pokaže da je preslikavanje
$$t\mapsto(\cos mt,\sin nt)$$iz $\mathbb{R}$ u $\mathbb{R}^2$, čija je slika Lissajousova krivulja, periodičko preslikavanje s periodom $\tau=2\pi$. Prema tome, da bismo iscrtali cijelu krivulju, dovoljno je uzeti broj $t$ iz omeđenog intervala $[0,2\pi)$. Lissajousove krivulje je stoga lako nacrtati uz pomoć raznih programa kao Matlab, Mathematica ili u programskim jezicima npr. C++, C$\#$, Java, koristeći odgovarajuće biblioteke za crtanje. Posebno je interesantno ako se iscrtavanje još k tome i animira.

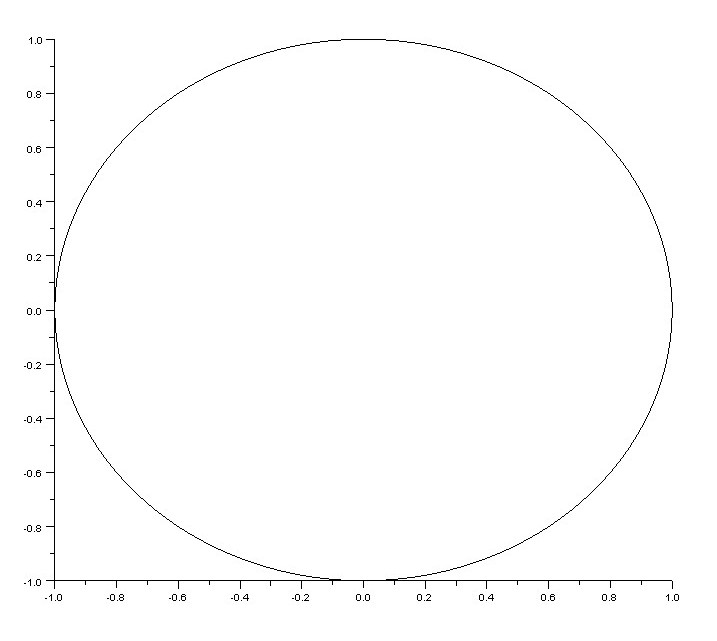
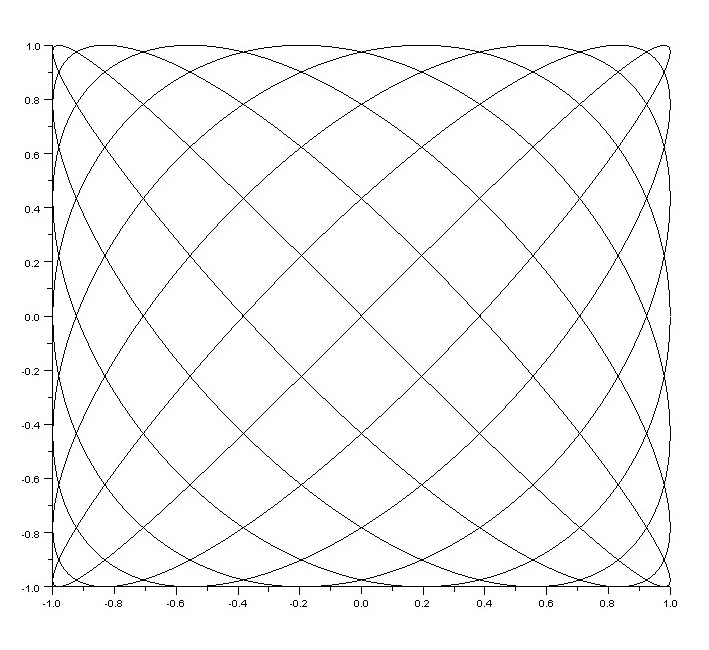
Evo nekoliko primjera Lissajousovih krivulja iscrtanih u programu Scilab (besplatna verzija Matlaba, vidi [1]):

$n = 1$, $m = 1$

$n = 7$, $m = 8$

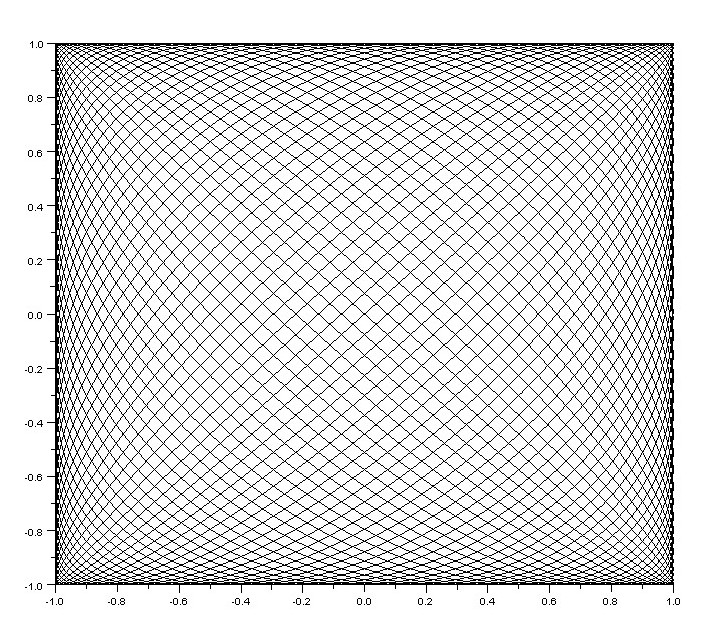
$n = 42$, $m = 41$

Sve Lissajousove krivulje se nalaze unutar kvadrata $[-1,1]^2$. Prva od krivulja je kružnica, koja ima parametarske jednadžbe: $x=\cos t$, $y=\sin t$, $t\in\mathbb{R}$.

Za određene parametre $m$, $n$ krivulja izgleda gusto. Međutim pod povećalom bi vidjeli velika prazna područja kroz koje krivulja ne prolazi. Matematički pojam gustoće je puno stroži od intuitivnog. U matematičkom smislu, nijedna od Lissajousovih krivulja s parametrima koji su prirodni brojevi, tj. $m$, $n\in\mathbb{N}$, nije gusta. O tome govori Teorem 2. Ako su $m$, $n$ nesumjerljivi realni brojevi, tj. $\frac mn\notin\mathbb{Q}$ (na pr. $m=1$, $n=\sqrt2$), i broj $t$ prolazi cijelim skupom $\mathbb{R}$, onda je dobivena Lissajousova krivulja gusta na kvadratu $[-1,1]\times[-1,1]$. O tome govori Teorem 1 koji ćemo uskoro dokazati.

Postoje u matematici i krajnje neintuitivne tzv. Peanove krivulje. One nastaju uzastopnim lomljenjem (bez kidanja) omeđenog intervala $[0,1]$, pri čemu tako nastala krivulja ispunjava cijeli kvadrat $[0,1]^2$. Lissajousove krivulje su glatke i ne mijenjaju brzo smjer, pa ih je lakše proučavati nego Peanove.

Matematički opis Lissajousovih krivulja

Definicija 1. Neka je $\alpha\in\mathbb{R}$, $\alpha\ne0$. Lissajousova krivulja je slika funkcije ${\cal L}:\mathbb{R}\to\mathbb{R}^2$, ${\cal L}(t)=(\cos t,\sin\alpha t)$, $t\in\mathbb{R}$. Parametarska jednadžba te krivulje je $$x=\cos t,\quad y=\sin\alpha t,\quad t\in\mathbb{R}.$$ Zbog $|\cos t|\le1$ i $|\sin t|\le1$, Lissajousova krivulja je podskup kvadrata $[-1,1]\times[-1,1]$.

Radi $(\cos(-t),\sin\alpha(-t))=(\cos t,\sin(-\alpha)t)$ s $\pm\alpha$ je određena ista Lissajousova krivulja. Dakle, bez smanjenja općenitosti, za Lissajousove krivulje možemo uzeti $\alpha>0$.

Ako je $\alpha\in\mathbb{Q}$, $\alpha=\frac mn$, $m$, $n\in\mathbb{N}$, zamjenom $t=n\,s$ dobijemo parametarski oblik Lissajousove krivulje s odvojenim parametrima:
$$
x=\cos ns,\quad y=\sin ms, \quad s\in\mathbb{R}.
$$

Propozicija 1. Neka je $\alpha\in\mathbb{R}$, $\alpha\ne0$. Funkcija ${\cal L}:\mathbb{R}\to\mathbb{R}^2$, $${\cal L}(t)=(\cos t,\sin\alpha t),\quad t\in\mathbb{R}$$je periodička onda i samo onda ako je $\alpha\in\mathbb{Q}$. Dakle, ako je Lissajousova krivulja slika funkcije zadane s $\alpha\in\mathbb{Q}$, $\alpha\ne0$, onda je ista krivulja slika i restrikcije funkcije ${\cal L}$ na neki omeđen interval (na pr. $[0,\tau]$, gdje je $\tau>0$ period funkcije ${\cal L}$).

Dokaz. Za $\alpha=\frac mn$, $m\in\mathbb{Z}$, $n\in\mathbb{N}$ je ${\cal L}(t+2n\pi)=\left(\cos(t+2n\pi), \sin\frac mn(t+2n\pi)\right)$ pa je ${\cal L}$ periodička funkcija s periodom $\tau=2n\pi>0$. Obratno, ako je ${\cal L}$ periodička funkcija s periodom $\tau>0$ onda je ${\cal L}(t+\tau)={\cal L}(t)$ za sve $t\in\mathbb{R}$, s tim da se radi o jednakosti točaka. Dakle vrijedi: $\cos(t+\tau)=\cos t$, $\sin(\alpha t+\alpha\tau)=\sin\alpha t$, za sve $t\in\mathbb{R}$. Iz prve jednakosti je $\tau=2n\pi$, $n\in\mathbb{N}$, a iz druge zbog $\alpha\ne0$$ slijedi $\alpha\tau=2m\pi$, $m\in\mathbb{Z}$, $m\ne0$. Dakle $\alpha\, 2n\pi=2m\pi$ tj. $\alpha=\frac mn$, jer je $n\ne0$. Q.E.D. (latinski "quod erat demonstrandum'' - "Što je trebalo dokazati''.)

Primjedba. Sinusoida je slika funkcije $S:\mathbb{R}\to\mathbb{R}^2$, $S(t)=(t,\sin t)$, $t\in\mathbb{R}$. Dakle slika jedne funkcije jednaka je grafu druge. Iako je $\sin$ periodička funkcija, lako se pokaže da funkcija $S$ to nije. Umjesto funkcije $\sin$, za konstrukciju funkcije $S$ mogli smo uzeti i bilo koju funkciju realne varijable. Funkcija $S$ nije periodička zbog prve koordinate od $S(t)$. Geometrijski razlog za to je ovaj: ako $t$ prolazi skupom $\mathbb{R}$ uvijek dobivamo nove i nove točke sinusoide bez povratka na stare točke.

Definicija 2. Skup $P\subset\mathbb{R}$ je gust na realnom pravcu, ako svaki (po volji male duljine) otvoreni interval $(a,b)$, $a$, $b\in\mathbb{R}$, $a<b$ sadrži bar jedan element skupa $P$. Primjer gustog skupa na pravcu je skup $\mathbb{Q}$ racionalnih brojeva.

Skup $P\subseteq S^1$ je gust na jediničnoj kružnici $S^1=\{z\in\mathbb{C}:|z|=1\}$ ako svaki otvoreni luk (po volji male lučne duljine) sadrži neku točku iz skupa $P$.

Skup $P\subseteq I^2$ je gust na pravokutniku $I^2=[-1,1]\times[-1,1]$, ako svaki otvoreni krug $K\subseteq I^2$ (po volji malog polumjera) uvijek sadrži i bar jednu točku iz skupa $P$.

Sada možemo iskazati ovaj teorem.

Teorem 1. Ako je $\alpha$ iracionalni broj, onda je Lissajousova krivulja $x=\cos t$, $y=\sin\alpha t$, $t\in\mathbb{R}$ gusta na kvadratu $[-1,1]^2$.

Dokaz teorema provodimo koristeći dvije leme. Osim toga koristimo i tzv. Eulerovu oznaku kojom se kompleksni broj $\cos\varphi+i\sin\varphi$ kratko zapisuje s $e^{i\varphi}$:
$$
e^{i\varphi}=\cos\varphi+i\sin\varphi.
$$Ta oznaka ima smisla jer Moivreova formula $$(\cos\varphi_1+i\sin\varphi_1)\,(\cos\varphi_2+i\sin\varphi_2)=
\cos(\varphi_1+\varphi_2)+i\sin(\varphi_1+\varphi_2)$$se tada kraće piše kao $$e^{i\varphi_1}\,e^{i\varphi_2}=e^{i(\varphi_1+\varphi_2)}$$što je osnovno svojstvo eksponencijalne funkcije. Primijetimo da je $e^x$ realan broj, a $e^{ix}$ kompleksni broj, i to na jediničnoj kružnici, ako je $x\in\mathbb{R}$. Također iz $e^{i\varphi}\,e^{i\alpha}=e^{i(\varphi+\alpha)}$ vidimo da množenje s kompleksnim brojem $e^{i\alpha}$ odgovara rotaciji točke $e^{i\varphi}$ na jediničnoj kružnici za kut $\alpha$. Na kraju
$$e^{i\varphi_1}=e^{i\varphi_2}\iff\varphi_1-\varphi_2=2k\pi,\quad k\in\mathbb{Z}.$$

Lema 1. Neka je $\alpha\in\mathbb{R}$, $\frac{\alpha}{2\pi}\notin\mathbb{Q}$, $\varphi\in\mathbb{R}_0$ i $S^1=\{z\in\mathbb{C}:|z|=1\}$ jedinična kružnica. Tada je skup $$P=\{e^{i(\varphi+k\alpha)}:k\in\mathbb{Z},\ k\ge0\}$$gust na $S^1$.

To znači da uzastopnim rotacijama bilo koje točke $z=e^{i\varphi}$ na kružnici za kutove $\alpha$, $2\alpha$, $3\alpha,\dots$, dobijemo skup točaka na kružnici koji siječe bilo koji po volji mali otvoreni luk na $S^1$.

Dokaz. Svi članovi niza
$$
e^{i\varphi},\ e^{i(\varphi+\alpha)},\ e^{i(\varphi+2\alpha)},\ e^{i(\varphi+3\alpha)},\dots
\tag1
$$su međusobno različiti brojevi. Naime, ako su $m$, $m'\in\mathbb{Z}$, $0\le m<m'$ i $e^{i(\varphi+m\alpha)}=e^{i(\varphi+m'\alpha)}$, onda je
$$
\quad (\varphi+m'\alpha)-(\varphi+m\alpha)=2k\pi,\ k\in\mathbb{Z}\quad\Longrightarrow\quad (m'-m)\alpha=2k\pi\quad \Longrightarrow\quad \frac{\alpha}{2\pi}=\frac{k}{m'-m}\in\mathbb{Q}
$$što je suprotno pretpostavci leme. Sada podijelimo kružnicu $S^1$ na $n$ jednakih poluotvorenih intervala duljine $\frac{2\pi}n$. Prema Dirichletovu principu među beskonačno (dakle i $n+1$) članova niza (1) postoje bar dva člana u istom poluotvorenom intervalu, dakle udaljena za manje od $\frac{2\pi}n$ na kružnici. Neka su to članovi $e^{i(\varphi+k\alpha)}$ i $e^{i(\varphi+l\alpha)}$, $k$, $l\in\mathbb{Z}$, $0\le k<l$.

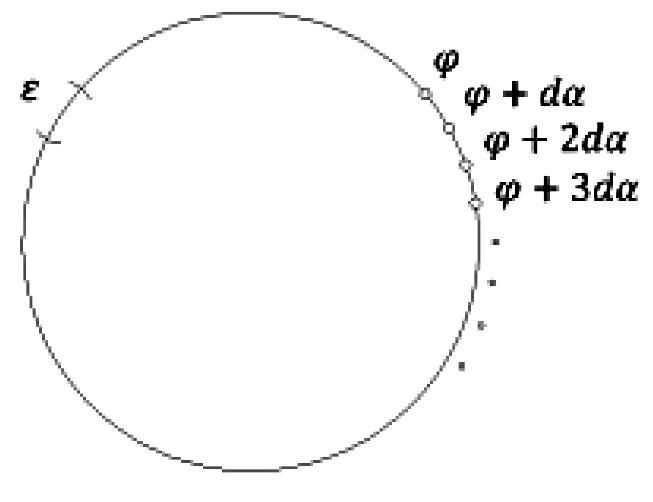
Neka je $d=l-k\in\mathbb{N}$. Sada iz $\frac{e^{i(\varphi+l\alpha)}}{e^{i(\varphi+k\alpha)}}=e^{id\alpha}$ vidimo da množenje s $e^{id\alpha}$ znači rotaciju (moguće i negativnu) za kut manji od $\frac{2\pi}n$. To znači da su u nizu točaka
$$
e^{i\varphi},\ e^{i(\varphi+d\alpha)},\ e^{i(\varphi+2d\alpha)},\ e^{i(\varphi+3d\alpha)},\dots
\tag2
$$svake dvije susjedne točke jednako udaljene na kružnici i to u lučnoj mjeri za manje od $\frac{2\pi}n$. Osim toga elementi niza (2) su elementi skupa $P$ iz Leme 1, jer je $d\in\mathbb{N}$.

Neka je sada na kružnici $S^1$ zadan otvoreni luk lučne duljine $\varepsilon>0$ i neka je $n\in\mathbb{N}$, takav da je $\frac{2\pi}n<\varepsilon$. Zbog svojstava niza (2) neki član tog niza će biti sigurno u tom luku. Q.E.D.

Lema 2. Neka je $\alpha\in\mathbb{R}$, $\frac{\alpha}{2\pi}\notin\mathbb{Q}$, $\varphi\in\mathbb{R}$, onda su skupovi
$$P_1=\{\cos(\varphi+k\alpha):k\in\mathbb{Z},\ k\ge0\}\quad\mbox{i}\quad P_2=\{\sin(\varphi+k\alpha):k\in\mathbb{Z},\ k\ge0\}$$gusti na intervalu $[-1,1]$.

Dokaz. Vrijedi $e^{i(\varphi+k\alpha)}=\cos(\varphi+k\alpha)+i\sin(\varphi+k\alpha)$.

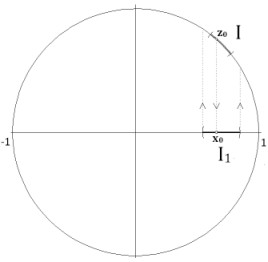
U intervalu $[-1,1]$ odaberemo bilo koji otvoreni interval $I_1$ duljine $\varepsilon>0$. Sada postoji otvoreni luk $I$ na kružnici koji se ortogonalno preslikava u $I_1$. Po Lemi 1 otvoreni luk $I$ sadrži točku oblika $z_0=e^{i(\varphi+k_0\alpha)}$, $k_0\in\mathbb{Z}$, $k_0\ge0$. To znači da je realni broj $x_0=\cos(\varphi+k_0\alpha)\in I_1$. Dakle skup $P_1$ je gust na $[-1,1]$. Analogan dokaz se provodi i za skup $P_2$. Q.E.D.

Dokaz Teorema 1. Neka je $\alpha$ iracionalni broj. Želimo dokazati da je tada Lissajousova krivulja
$$x=\cos t,\quad y=\sin\alpha t$$gusta na kvadratu $I^2=[-1,1]^2$.

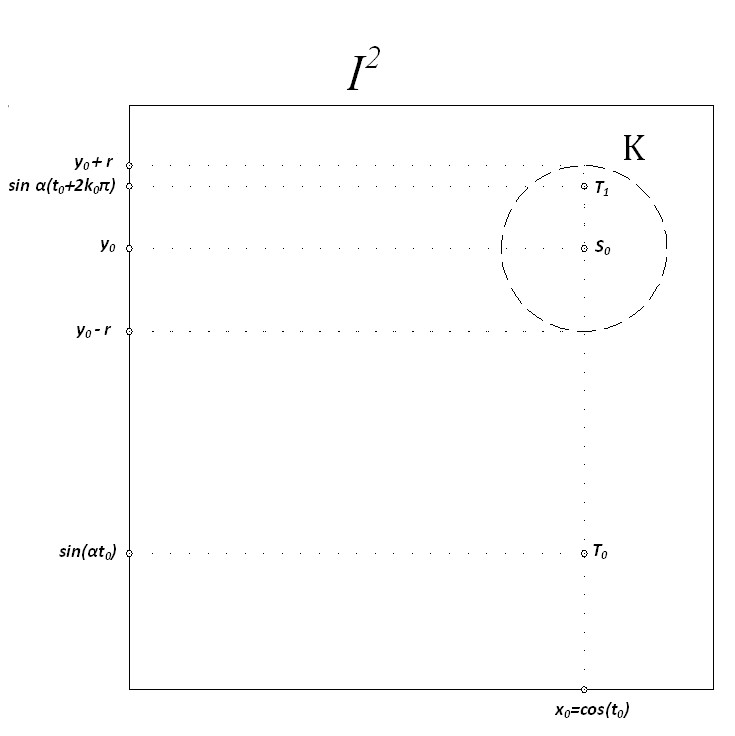
Neka je $K(S_0,r)\subseteq[-1,1]^2$ otvoreni krug po volji malog polumjera $r>0$, sa središtem $S_0(x_0,y_0)$. Budući da je $\cos:\mathbb{R}\to[-1,1]$ surjekcija, to postoji $t_0\in\mathbb{R}$ tako da je $x_0=\cos t_0$. Primijetimo da broj $\sin\alpha t_0$ ne mora biti u intervalu $(y_0-r,y_0+r)$, odnosno točka $$T_0(\cos t_0,\sin\alpha t_0)$ Lissajousove krivulje ne mora biti u $K(S_0,r)$. Sada promatramo skup brojeva
$$
\begin{aligned}
\{\sin\alpha(t_0+2k\pi):k\in\mathbb{Z},\ k\ge0\}&=\{\sin(\alpha t_0+k\,2\pi\alpha):k\in\mathbb{Z},\ k\ge0\}\\
&=\{\sin(\varphi+k\beta):k\in\mathbb{Z},\ k\ge0\}
\end{aligned}
$$gdje smo zamijenili $\varphi=\alpha t_0$, $\beta=2\pi\alpha$, $\frac{\beta}{2\pi}=\alpha\notin\mathbb{Q}$. Po Lemi 2 postoji $k_0\in\mathbb{Z}$, $k_0\ge0$ tako da je $\sin\alpha(t_0+2k_0\pi)\in(y_0-r,y_0+r)$. Zbog periodičnosti kosinusa je točka Lissajousove krivulje $T_1=(\cos(t_0+2k_0\pi), \sin\alpha(t_0+2k_0\pi))=(x_0,\sin\alpha(t_0+2k_0\pi))\in K(S_0,r)$. Q.E.D.

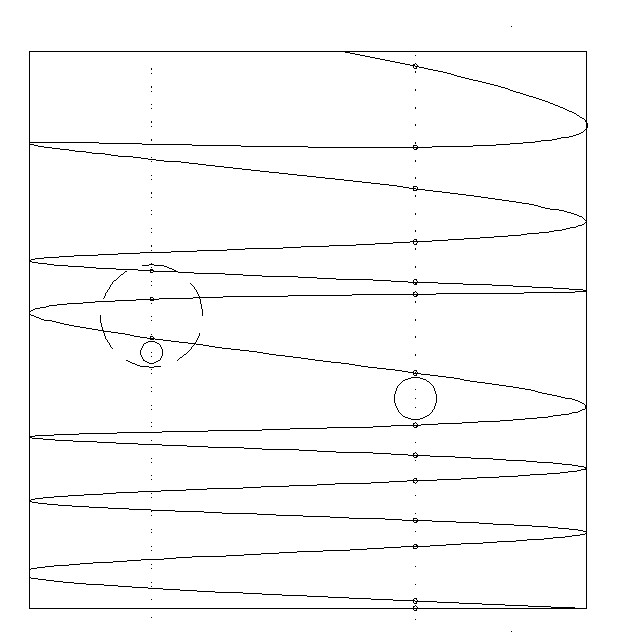
Da Lissajousova krivulja nije gusta na kvadratu $[-1,1]^2$, znači da postoji bar jedan otvoreni krug $K\subseteq[-1,1]^2$ koji ne sadrži nijednu točku Lissajousove krivulje. Za $\alpha\in\mathbb{Q}$ sljedeći teorem, koji ovdje nećemo dokazivati, daje i više od toga.

Teorem 2. Ako je $\alpha\in\mathbb{Q}$, onda Lissajousova krivulja $x=\cos t$, $y=\sin\alpha t$ nije gusta na kvadratu $I^2=[-1,1]^2$. Preciznije, vrijedi:

Svaka paralela s $y$-osi siječe Lissajousovu krivulju u najviše konačno mnogo točaka. Dakle postoje točke otvorenog kvadrata $(-1,1)^2$ koje nisu na Lissajousovoj krivulji.
Oko svake točke otvorenog kvadrata koja nije na Lissajousovoj krivulji postoji otvoreni krug $K\subseteq I^2$ koji ne siječe Lissajousovu krivulju.
Skup svih točaka kvadrata $I^2$ koje ne leže na Lissajousovoj krivulji je gust na kvadratu $I^2$, ali vrijedi i više od toga: svaki otvoreni krug $K\subseteq I^2$ sadrži i cijeli krug koji ne siječe Lissajousovu krivulju.

Literatura

Program Scilab možete pronaći na adresi http://www.scilab.org/. Za kreiranje Lissajousove krivulje možete koristiti naredbu: xbasc; x=0:0.001:2*%pi; plot2d(cos(41*x),sin(42*x));. Naredba se izvrši pritiskom na tipku Enter.
Informacije o Lissajousovim krivuljama možete naći i na: http://en.wikipedia.org/wiki/Lissajous\char95curve te http://mathworld.wolfram.com/LissajousCurve.html
D. Veljan, Kombinatorika s teorijom grafova, Školska knjiga, Zagreb, 1989. Dokaz Leme 1 iz ovog članka je na str. 56, a Teorem 1 je postavljen kao zadatak 33 na str. 72.

Na portalu www.krunopopovic.com ćete pronaći lijepi alat za crtanje Lissajousovih krivulja, koji je izradio prof. Krunoslav Popović.

Ovaj program omogućava uz pomoć klizača mijenjate parametre $m$ i $n$ koji određuju Lissajousovu krivulju: www.krunopopovic.com/lissas3.swf

Članak je objavljen u Matematičko-fizičkom listu LX 2 (2009.-2010.), str. 75-79. Zahvaljujemo autoru prof. Krunoslavu Popoviću i glavnom uredniku MFL-a dr. Željku Hanjšu na dopuštenju da članak bude objavljen na ovom webu. Također zahvaljujemo poduzeću ELEMENT na poslanom $\LaTeX$-izvorniku. Za web priredio Darko Žubrinić 2012.

Zavod za primijenjenu matematiku FER-a
Sveučilište u Zagrebu